题目内容
3.[x]表示不超过x的最大整数,如[-2.1]=-3,[π]=3,[0]=0,求函数y=|$\frac{1}{x}$-[$\frac{1}{x}$+$\frac{1}{2}$]|的最大值,并求此时的x值.分析 首先设[$\frac{1}{x}$+$\frac{1}{2}$]=n,得出$\frac{1}{x}$+$\frac{1}{2}$=n+a(0≤a<1)m,进而得出当a=0时,y最大=$\frac{1}{2}$,求出x的值即可.
解答 解:设[$\frac{1}{x}$+$\frac{1}{2}$]=n,
则$\frac{1}{x}$+$\frac{1}{2}$=n+a(0≤a<1),
则y=|n+a-$\frac{1}{2}$-n|=|a-$\frac{1}{2}$|,
当a=0时,y最大=$\frac{1}{2}$,
则x=$\frac{2}{2n-1}$(n为整数),
故此时$\frac{1}{x}$+$\frac{1}{2}$是整数,
则x=2.
点评 此题主要考查了取整计算,正确利用已知结合绝对值的性质得出是解题关键.

练习册系列答案
相关题目
14.下列各图是电视台的台徽,其中是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.如果25x2-kxy+49y2是一个完全平方式,那么k的值是( )
| A. | 1225 | B. | 35 | C. | -70 | D. | ±70 |
8. 如图,a∥b,∠1=120°,则∠2等于( )
如图,a∥b,∠1=120°,则∠2等于( )
 如图,a∥b,∠1=120°,则∠2等于( )
如图,a∥b,∠1=120°,则∠2等于( )| A. | 30° | B. | 90° | C. | 60° | D. | 50° |
15.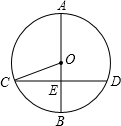 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么sin∠OCE=( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么sin∠OCE=( )
 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么sin∠OCE=( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么sin∠OCE=( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
 根据下图所示的程序计算,若输入的x的值为1,则输出的y的值是多少?
根据下图所示的程序计算,若输入的x的值为1,则输出的y的值是多少?