题目内容
20. 如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F在AD上,若△ABC的面积为16cm2,则图中阴影部分的面积为8cm2.
如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F在AD上,若△ABC的面积为16cm2,则图中阴影部分的面积为8cm2.
分析 根据等腰三角形的性质由AB=AC,AD⊥DC得出BD=CD,利用同底等高得到S△BEF=S△CEF,则S阴影部分=S△ABD=$\frac{1}{2}$S△ABC,利用△ABC的面积为16cm2即可得到阴影部分的面积.
解答 解:∵AB=AC,AD⊥DC,
∴BD=CD,
∴S△BEF=S△CEF,
∴S阴影部分=S△ABD=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×16=8(cm2).
故答案为:8.
点评 本题考查了等腰三角形的性质:等腰三角形顶角的角平分线垂直平分底边.也考查了三角形的面积公式.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
10.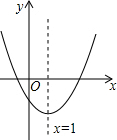 已知y=ax2+bx+c(a≠0)在平面直角坐标系中的图象如图所示,则下列结论正确的是( )
已知y=ax2+bx+c(a≠0)在平面直角坐标系中的图象如图所示,则下列结论正确的是( )
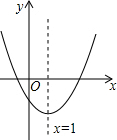 已知y=ax2+bx+c(a≠0)在平面直角坐标系中的图象如图所示,则下列结论正确的是( )
已知y=ax2+bx+c(a≠0)在平面直角坐标系中的图象如图所示,则下列结论正确的是( )| A. | a<0 | B. | c>0 | C. | 2a+b=0 | D. | 4a+2b+c>0 |
8. 如图,a∥b,∠1=120°,则∠2等于( )
如图,a∥b,∠1=120°,则∠2等于( )
 如图,a∥b,∠1=120°,则∠2等于( )
如图,a∥b,∠1=120°,则∠2等于( )| A. | 30° | B. | 90° | C. | 60° | D. | 50° |
15.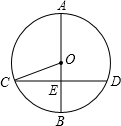 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么sin∠OCE=( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么sin∠OCE=( )
 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么sin∠OCE=( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么sin∠OCE=( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
 如图,在边长为a cm的正方形内,截去两个以正方形的边长a cm为直径的半圆,则
如图,在边长为a cm的正方形内,截去两个以正方形的边长a cm为直径的半圆,则 根据下图所示的程序计算,若输入的x的值为1,则输出的y的值是多少?
根据下图所示的程序计算,若输入的x的值为1,则输出的y的值是多少? 如图,△ABC≌△ADE,∠E=∠DAB,找出图中平行的两条线段,并说明理由.
如图,△ABC≌△ADE,∠E=∠DAB,找出图中平行的两条线段,并说明理由.