题目内容
2.①把抛物线y=-x2-2x-3 向右移3个单位,向下移5个单位,可以得到抛物线y=-x2+4x-3;②抛物线y=2x2-4x-3关于x轴对称的抛物线的解析式y=-2x2+4x+3;
③抛物线y=-3x2-4x+1关于y轴对称的抛物线的解析式y=-3x2+4x+1.
分析 ①求得平移后抛物线的顶点坐标,根据平移规律得到原抛物线的顶点坐标,由此写出原抛物线的解析式;
②先把抛物线解析式配成顶点式,然后写出顶点关于x轴对称的点,把它作为所求抛物线的顶点,二次项系数与原来互为相反数,这样就可确定对称后抛物线的解析式;
③先把抛物线解析式配成顶点式,然后写出顶点关于y轴对称的点,把它作为所求抛物线的顶点,二次项系数不变,这样就可确定对称后抛物线的解析式.
解答 解:①y=-x2+4x-3=-(x-2)2-7,则该抛物线的顶点坐标为(2,-7),
将其向左平移3个单位,向上平移5个单位后的坐标是(-1,-2),
所以原抛物线的解析式为:y=-(x+1)2-2=-x2-2x-3.
故答案是:y=-x2-2x-3;
②∵y=2x2-4x-3=2(x-1)2-5,顶点坐标为(1,-5),
(1,-5)关于x轴对称的点的坐标为(1,5),
而两抛物线关于x轴对称时形状不变,只是开口方向相反,
∴抛物线y=2x2-4x-3关于x轴对称的抛物线的解析式为y=-2(x-1)2+5=-2x2+4x+3.
故答案为:y=-2x2+4x+3;
③y=-3x2-4x+1=-3(x+$\frac{2}{3}$)2+$\frac{7}{3}$,则该抛物线的顶点坐标为(-$\frac{2}{3}$,$\frac{7}{3}$).
该顶点关于y轴对称的坐标为($\frac{2}{3}$,$\frac{7}{3}$),
所以抛物线y=-3x2-4x+1关于y轴对称的抛物线的解析式为:y=-3(x-$\frac{2}{3}$)2+$\frac{7}{3}$=-3x2+4x+1.
故答案是:y=-3x2+4x+1.
点评 主要考查了二次函数图象与几何变换,抛物线平移问题,实际上就是两条抛物线顶点之间的问题,找到了顶点的变化就知道了抛物线的变化.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案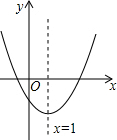 已知y=ax2+bx+c(a≠0)在平面直角坐标系中的图象如图所示,则下列结论正确的是( )
已知y=ax2+bx+c(a≠0)在平面直角坐标系中的图象如图所示,则下列结论正确的是( )| A. | a<0 | B. | c>0 | C. | 2a+b=0 | D. | 4a+2b+c>0 |
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y2>y3>y1 | D. | y3>y1>y2 |
| A. |  | B. |  | C. |  | D. |  |
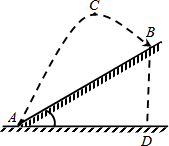 如图,在高尔夫球赛中,运动员从山坡下A处打出一球向山坡上洞B飞去,已知山坡的坡角为30°,AB=18m,球的飞行的水平距离为9m时达到最大高度12m的C处,若球的飞行轨迹为抛物线,问运动员能否一杆入洞?
如图,在高尔夫球赛中,运动员从山坡下A处打出一球向山坡上洞B飞去,已知山坡的坡角为30°,AB=18m,球的飞行的水平距离为9m时达到最大高度12m的C处,若球的飞行轨迹为抛物线,问运动员能否一杆入洞? 根据下图所示的程序计算,若输入的x的值为1,则输出的y的值是多少?
根据下图所示的程序计算,若输入的x的值为1,则输出的y的值是多少?