题目内容
20.已知m、n、p分别是Rt△ABC的三边长,且m≤n<p.(1)求证:关于x的一元二次方程mx2+$\sqrt{2}$px+n=0必有实数根;
(2)若x=-1是一元二次方程mx2+$\sqrt{2}$px+n=0的一个根,且Rt△ABC的周长为2$\sqrt{2}$+2,求Rt△ABC的面积.
分析 (1)计算根的判别式和勾股定理两者结合得出答案即可;
(2)由若x=-1是一元二次方程mx2+$\sqrt{2}$px+n=0的一个根,且Rt△ABC的周长为2$\sqrt{2}$+2,结合m≤n<p推出mn的乘积即可得出结论.
解答 (1)证明:∵m、n、p分别是Rt△ABC的三边长,且m≤n<p,
∴p2=m2+n2,
∴b2-4ac=2p2-4mn=2(m2+n2)-4mn=2(m-n)2≥0,
∴关于x的一元二次方程mx2+$\sqrt{2}$px+n=0必有实数根;
(2)解:∵x=-1是一元二次方程mx2+$\sqrt{2}$px+n=0的一个根,
∴m-$\sqrt{2}$p+n=0①,
∵Rt△ABC的周长为2$\sqrt{2}$+2,
∴m+n+p=2$\sqrt{2}$+2②,
由①、②得:m+n=2$\sqrt{2}$,p=2,
∴(m+n)2=8,
∴m2+2mn+n2=8,
又∵m2+n2=p2=4,
∴2mn=4,
∴$\frac{1}{2}$mn=1,
∴Rt△ABC的面积是1.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.根据等式的性质7=5x-2可变形为( )
| A. | -5x=2-7 | B. | -5x=-2+7 | C. | 7-2=5x | D. | 7+2=5x |
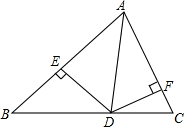 △ABC中,AD为角平分线,DE⊥AB于E,DF⊥AC于F,AB=10cm,AC=8cm,△ABC的面积为54cm2,求DE的长.
△ABC中,AD为角平分线,DE⊥AB于E,DF⊥AC于F,AB=10cm,AC=8cm,△ABC的面积为54cm2,求DE的长.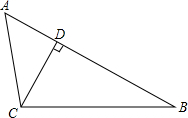 如图所示,在△ABC中,CD是AB边上的高,且AC•BD=BC•CD.求证:
如图所示,在△ABC中,CD是AB边上的高,且AC•BD=BC•CD.求证: