题目内容
17. 如图,AB∥CD,EF⊥DF,∠D:∠E:∠B=4:2:1,求∠E的度数.
如图,AB∥CD,EF⊥DF,∠D:∠E:∠B=4:2:1,求∠E的度数.
分析 延长BE交DC于M,设∠B=x,则∠BEF=2x,∠D=4x,∠MEF=180°-2x,由平行线的性质得出∠1=∠B=x,在四边形EFDM中,由四边形内角和定理得出方程,解方程求出x,即可得出结果.
解答 解:延长BE交DC于M,如图所示:
设∠B=x,则∠BEF=2x,∠D=4x,
∴∠MEF=180°-2x,
∵AB∥CD,
∴∠1=∠B=x,
∵EF⊥DF,
∴∠F=90°,
在四边形EFDM中,由四边形内角和定理得:
x+4x+90°+180°-2x=360°,
解得:x=30°,
∴∠BEF=60°.
点评 本题考查了平行线的性质、四边形内角和定理;熟练掌握平行线的性质,由四边形内角和定理得出方程是解决问题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
8.根据等式的性质7=5x-2可变形为( )
| A. | -5x=2-7 | B. | -5x=-2+7 | C. | 7-2=5x | D. | 7+2=5x |
 如图,在△ABC中,AB=AC,BD=BC,AD=DE=BE.
如图,在△ABC中,AB=AC,BD=BC,AD=DE=BE.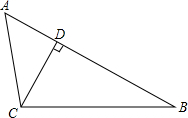 如图所示,在△ABC中,CD是AB边上的高,且AC•BD=BC•CD.求证:
如图所示,在△ABC中,CD是AB边上的高,且AC•BD=BC•CD.求证: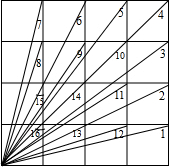 如图,是一个4×4的方格,
如图,是一个4×4的方格,