Question

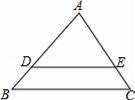
如图所示，AB为半圆O的直径，点D是半圆弧的中点，半径OC∥BD，过点C作AD的平行线交BA延长线于点E．

（1）判断CE与半圆OD的位置关系，并证明你的结论．

（2）若BD=4，求阴影部分面积．

Answer 1

【考点】切线的判定；扇形面积的计算．

【分析】（1）直接利用圆周角定理结合平行线的性质得出CO⊥EC，即可得出答案；

（2）利用已知得出△ADB为等腰直角三角形，进而得出△ECO为等腰直角三角形，由S_阴影部分=S_△ECD﹣S_扇形AOC求出答案．

【解答】解：（1）CE与半圆OD相切，

理由：∵AB为直径，

∴∠ADB=90°，

∴AD⊥DB，

∵CO∥DB，

∴CO⊥AD，

∵EC∥AD，

∴CO⊥EC，

∴CE与半圆OD相切；

 

（2）∵点D平分半圆弧，

∴∠B=45°，

∴△ADB为等腰直角三角形，

∵BD=4，

∴AB=4，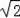

∴CO=2，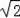

∵CO∥DB，

∴∠AOC=∠ABD=45°，

由（1）知CO⊥EC，

∴△ECO为等腰直角三角形，

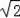
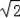
∴S_阴影部分=S_△ECD﹣S_扇形AOC=（2）²﹣π（2）²=4﹣π．

【点评】此题主要考查了切线的判定以及等腰直角三角形的性质、扇形面积求法等知识，正确得出△ECO为等腰直角三角形是解题关键．