题目内容
1．某校组织了主题为“让勤俭节约成为时尚”的电子小组作品征集活动，现从中随机抽取部分作品，对其份数和成绩（十分制）进行整理，制成了如下两幅不完整的统计图．（1）求本次抽取的作品数量并补全条形统计图；
（2）此次被抽取的作品的平均得分是8.05分．
（3）若该校共征集到800份作品，请估计8分的作品约有多少份？
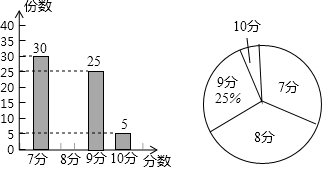
分析 （1）根据9分的人数除以占的百分比，得到抽取作品的总份数补全条形统计图即可；
（2）根据题意列式即可得到平均分；
（3）求出8分占的百分比，乘以800即可得到结果．
解答 
解：（1）本次抽取的作品数量是：25÷25%=100（份）；
补全条形统计图如图所示，
（2）此次被抽取的作品的平均得分是：$\frac{7×30+40×8+9×25+10×5}{100}$=8.05分；
故答案为：8.05；
（3）800×$\frac{40}{100}$=320（份），
答：8分的作品约有320份．
点评 此题考查了条形统计图，扇形统计图，以及用样本估计总体，弄清题意是解本题的关键．
练习册系列答案
相关题目
11．某网店3月份经营一种热销商品，每件成本20元，发现三周内售价在持续提升，销售单价P（元/件）与时间t（天）之间的函数关系为P=30+$\frac{1}{4}$t（其中1≤t≤21，t为整数），且其日销售量y（件）与时间t（天）的关系如下表
（1）已知y与t之间的变化规律符合一次函数关系，请直接写出y（件）与时间t（天）函数关系式；
（2）在这三周的销售中，第几天的销售利润最大？最大日销售利润为多少？
（3）在实际销售的21天中，该网店每销售一件商品就捐赠a元利润（a＜8）给“精准扶贫”的对象，通过销售记录发现，这21天中，每天扣除捐赠后的日销售利润随时间t（天）的增大而增大，求a的取值范围．
| 时间t（天） | 1 | 5 | 9 | 13 | 17 | 21 |
| 日销售量y（件） | 118 | 110 | 102 | 94 | 86 | 78 |
（2）在这三周的销售中，第几天的销售利润最大？最大日销售利润为多少？
（3）在实际销售的21天中，该网店每销售一件商品就捐赠a元利润（a＜8）给“精准扶贫”的对象，通过销售记录发现，这21天中，每天扣除捐赠后的日销售利润随时间t（天）的增大而增大，求a的取值范围．
一次函数y=-3x+b和y=kx+1的图象如图所示，其交点为P（3，4），则不等式（3+k）x≥b-1的解集是x≥3．
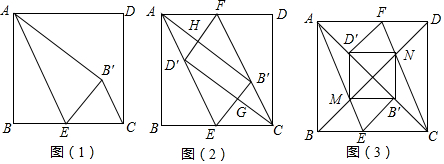
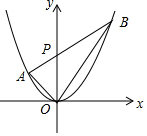若三角形的一边和该边上的高相等的三角形称为“和谐三角形”，如图，已知抛物线y=ax2经过A（-1，1），P是y轴正半轴上的动点，射线AP与抛物线交于另一点B，当△AOP是“和谐三角形”时，点B的坐标为（2，4）和（1，1）．
10．将28°42′31″保留到“′”为（ ）
| A． | 28°42′ | B． | 28°43′ | C． | 28°42′30″ | D． | 29°00′ |
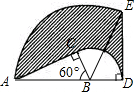如图，在△ABC中，∠ACB=90°，∠ABC=60°，AB=12cm，将△ABC以点B为中心顺时针旋转，使点C旋转到AB边延长线上的点D处，则AC边扫过的图形（阴影部分）的面积是36πcm2．（结果保留π）．