题目内容
9.某居民区道路上的“早市”引起了大家关注,小明想了解本小区居民对“早市”的看法,进行了一次抽样调查,把居民对“早市”的看法分为四个层次:A、非常赞同B、赞同但要有一定的限制;C、无所谓D、不赞同,并将调查结果绘制了图1和图2两幅不完整的统计图.
请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“早市”的看法表示赞同(包括A层次).
分析 (1)根据A层次的有90人,所占的百分比是30%,据此即可求得调查的总人数;
(2)利用总人数乘以对应的百分比求得C层次的人数,然后用总人数减去其它层次的人数求得B层次的人数,从而补全直方图;
(3)利用360°乘以对应的百分比求得所在扇形的圆心角的度数;
(4)利用总人数乘以对应的比例即可求解.
解答 解:(1)抽查的总人数是90÷30%=300(人);
(2)C层次的人数是300×20%=60(人),
则B层次的人数是300-90-60-30=120(人),所占的百分比是$\frac{120}{300}$=40%,
D层次所占的百分比是$\frac{30}{300}$=10%.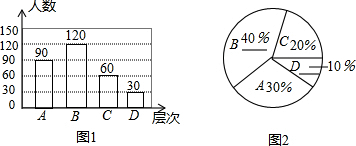 ;
;
(3)“C”层次所在扇形的圆心角的度数是360°×$\frac{60}{300}$=72°;
(4)对“早市”的看法表示赞同(包括A层次和B层次)的大约有4000×$\frac{90+120}{300}$=2800(人).
答:估计对“早市”的看法表示赞同(包括A层次和B层次).表示赞同的大约有2800人.
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
19.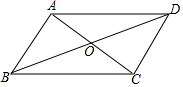 如图,已知平行四边形ABCD的对角钱AC与BD相交于点O,AB⊥AC,若AB=2,AC=8,则对角线BD的长是( )
如图,已知平行四边形ABCD的对角钱AC与BD相交于点O,AB⊥AC,若AB=2,AC=8,则对角线BD的长是( )
 如图,已知平行四边形ABCD的对角钱AC与BD相交于点O,AB⊥AC,若AB=2,AC=8,则对角线BD的长是( )
如图,已知平行四边形ABCD的对角钱AC与BD相交于点O,AB⊥AC,若AB=2,AC=8,则对角线BD的长是( )| A. | 4$\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
19. 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,那么∠1的度数是( )
如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,那么∠1的度数是( )
 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,那么∠1的度数是( )
如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,那么∠1的度数是( )| A. | 52° | B. | 38° | C. | 42° | D. | 62° |
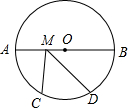 如图,⊙O的半径是8,AB是⊙O的直径,M为AB上一动点,$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$,则CM+DM的最小值为16.
如图,⊙O的半径是8,AB是⊙O的直径,M为AB上一动点,$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$,则CM+DM的最小值为16.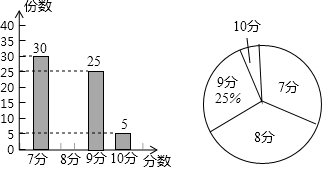
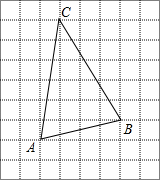 如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.