题目内容
20.如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,(1)方程x2-x-2=0不是(填“是”或“不是”)倍根方程;
(2)若(x-2)(mx+n)=0是倍根方程,则求代数式4m2+5mn+n2值;
(3)若点(p,q)在反比例函数y=$\frac{2}{x}$的图象上,则关于x的方程px2+3x+q=0是倍根方程吗?
分析 (1)解得方程后即可利用倍根方程的定义进行判断;
(2)根据(x-2)(mx+n)=0是倍根方程,从而得到m+n=0,4m+n=0,进而得到4m2+5mn+n2=(4m+n)(m+n)=0;
(3)根据点(p,q)在反比例函数y=的图象上得到pq=2,然后解方程px2+3x+q=0即可得到正确的结论.
解答 解:(1)解方程x2-x-2=0得:x1=2,x2=-1,
∴方程x2-x-2=0不是倍根方程,
故答案为:不是;
(2)∵(x-2)(mx+n)=0是倍根方程,且x1=2,x2=-$\frac{n}{m}$,
∴$\frac{n}{m}$=-1,或$\frac{n}{m}$=-4,
∴m+n=0,4m+n=0,
∵4m2+5mn+n2=(4m+n)(m+n)=0;
(3)关于x的方程px2+3x+q=0是倍根方程,理由如下:
∵点(p,q)在反比例函数y=$\frac{2}{x}$的图象上,
∴pq=2,
解方程px2+3x+q=0得:x1=-$\frac{1}{p}$,x2=-$\frac{2}{p}$,
∴x2=2x1,
∴关于x的方程px2+3x+q=0是倍根方程.
点评 本题考查了一元二次方程的解,根与系数的关系,根的判别式,反比例函数图形上点的坐标特征,正确的理解“倍根方程”的定义是解题的关键.

练习册系列答案
相关题目
11.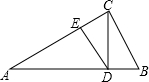 如图,在Rt△ABC中,BC=a,AB=c,CD为斜边上的高,DE⊥AC.设△AED、△CDB、△ABC的周长分别为p1,p2,p,则当$\frac{{p}_{1}+{p}_{2}}{p}$取最大值时,sinA=( )
如图,在Rt△ABC中,BC=a,AB=c,CD为斜边上的高,DE⊥AC.设△AED、△CDB、△ABC的周长分别为p1,p2,p,则当$\frac{{p}_{1}+{p}_{2}}{p}$取最大值时,sinA=( )
 如图,在Rt△ABC中,BC=a,AB=c,CD为斜边上的高,DE⊥AC.设△AED、△CDB、△ABC的周长分别为p1,p2,p,则当$\frac{{p}_{1}+{p}_{2}}{p}$取最大值时,sinA=( )
如图,在Rt△ABC中,BC=a,AB=c,CD为斜边上的高,DE⊥AC.设△AED、△CDB、△ABC的周长分别为p1,p2,p,则当$\frac{{p}_{1}+{p}_{2}}{p}$取最大值时,sinA=( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{3}{4}$ |
9. 下列三角形中,一定和△ABC全等的是( )
下列三角形中,一定和△ABC全等的是( )
 下列三角形中,一定和△ABC全等的是( )
下列三角形中,一定和△ABC全等的是( )| A. |  | B. |  | C. |  | D. |  |

 如图,在平面直角坐标系中,⊙P的半径为4,圆心P坐标是(4,a)(a>4),函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{3}$,则a的值是4+2$\sqrt{2}$.
如图,在平面直角坐标系中,⊙P的半径为4,圆心P坐标是(4,a)(a>4),函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{3}$,则a的值是4+2$\sqrt{2}$. 如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )