题目内容
12.若关于x、y的代数式2x2+ax-y+6-2bx2+3x-5y+2015的值与字母x的取值无关,求:3a2-6ab-3b2-4a2-ab-b2的值.分析 原式合并同类项得到最简结果,由结果与x取值无关确定出a与b的值,代入原式计算即可得到结果.
解答 解:2x2+ax-y+6-2bx2+3x-5y+2015=(2-2b)x2+(a+3)x-6y+2021,
由结果与x取值无关,得到2-2b=0,a+3=0,
解得:a=-3,b=1,
则原式=-a2-7ab-4b2=-9+21-4=8.
点评 此题考查了多项式,熟练掌握合并同类项法则是解本题的关键.

练习册系列答案
相关题目
7. 如图,C、D是以AB为直径的圆O上的两个动点(点C、D不与A、B重合),在运动过程中弦CD始终保持不变,M是弦CD的中点,过点C作CP⊥AB于点P.若CD=3,AB=5,PM=x,则x的最大值是( )
如图,C、D是以AB为直径的圆O上的两个动点(点C、D不与A、B重合),在运动过程中弦CD始终保持不变,M是弦CD的中点,过点C作CP⊥AB于点P.若CD=3,AB=5,PM=x,则x的最大值是( )
 如图,C、D是以AB为直径的圆O上的两个动点(点C、D不与A、B重合),在运动过程中弦CD始终保持不变,M是弦CD的中点,过点C作CP⊥AB于点P.若CD=3,AB=5,PM=x,则x的最大值是( )
如图,C、D是以AB为直径的圆O上的两个动点(点C、D不与A、B重合),在运动过程中弦CD始终保持不变,M是弦CD的中点,过点C作CP⊥AB于点P.若CD=3,AB=5,PM=x,则x的最大值是( )| A. | 3 | B. | $\sqrt{5}$ | C. | 2.5 | D. | 2$\sqrt{3}$ |
17. 如图,矩形ABCD的外接圆O与水平地面有唯一交点A,圆O的半径为4,且$\widehat{BC}$=2$\widehat{AB}$.若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了98π,则此时该圆与地面交点在( )上.
如图,矩形ABCD的外接圆O与水平地面有唯一交点A,圆O的半径为4,且$\widehat{BC}$=2$\widehat{AB}$.若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了98π,则此时该圆与地面交点在( )上.
 如图,矩形ABCD的外接圆O与水平地面有唯一交点A,圆O的半径为4,且$\widehat{BC}$=2$\widehat{AB}$.若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了98π,则此时该圆与地面交点在( )上.
如图,矩形ABCD的外接圆O与水平地面有唯一交点A,圆O的半径为4,且$\widehat{BC}$=2$\widehat{AB}$.若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了98π,则此时该圆与地面交点在( )上.| A. | $\widehat{AB}$ | B. | $\widehat{BC}$ | C. | $\widehat{CD}$ | D. | $\widehat{DA}$ |
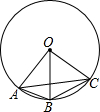 如图,点A、B、C均在⊙O上,且AB∥OC,若⊙O的半径为5,BC=6,则AC=8.
如图,点A、B、C均在⊙O上,且AB∥OC,若⊙O的半径为5,BC=6,则AC=8. 将如图所示的图形面积分成相等的两部分.
将如图所示的图形面积分成相等的两部分. 如图所示,直线m是一次函数y=kx+b的图象.
如图所示,直线m是一次函数y=kx+b的图象.