题目内容
17. 已知,如图,在△ABC中,AD是BC边上的中线,E是AD上的一点,AE=2DE,AE=3,BE=4,CE=5,求△ABC的面积.
已知,如图,在△ABC中,AD是BC边上的中线,E是AD上的一点,AE=2DE,AE=3,BE=4,CE=5,求△ABC的面积.
分析 延长AD到F,使ED=DF,连接BF,于是得到EF=AE=3,通过△BDF≌△CDE,得到BF=CE=5,根据勾股定理的逆定理得到∠BEF=90°,于是求得S△BCE=2S△BEF=2×$\frac{1}{2}$×3×4=12,由于AE=2DE,于是得到S△ABE+S△ACE=2S△BCE=24,即可得到结论.
解答  解:延长AD到F,使ED=DF,连接BF,
解:延长AD到F,使ED=DF,连接BF,
∴EF=2DE,
∵AE=2DE,AE=3,
∴EF=AE=3,
在△BDF与△CED中,$\left\{\begin{array}{l}{BD=CD}\\{∠BDF=∠CDE}\\{DE=DF}\end{array}\right.$,
∴△BDF≌△CDE,
∴BF=CE=5,
∵BE=4,
∴BE2+EF2=42+32=52=BF2,
∴∠BEF=90°,
∴S△BCE=S△BEF=$\frac{1}{2}$×3×4=6,
∵AE=2DE,
∴S△ABE+S△ACE=2S△BCE=12,
∴S△ABC=18.
点评 本题考查了全等三角形的判定和性质,勾股定理及逆定理,三角形的面积,熟练掌握勾股定理的逆定理是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.多项式x3y2-5x2y+6xy-3的次数是( )
| A. | 2 | B. | 3 | C. | 5 | D. | 10 |
12.已知代数式a2+4a-2的值为3,则代数式a-1的值为( )
| A. | -5或1 | B. | -6或0 | C. | 0 | D. | -6 |
6.从正方形铁片的一边截去2cm宽的一条长方形铁片,再从剩余部分的短边截去3cm宽的一条长方形铁片,余下的面积是42cm2,则原来的正方形铁片的面积是( )
| A. | 6cm2 | B. | 16cm2 | C. | 64cm2 | D. | 81cm2 |
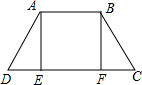 如图所示,四边形ABCD是一条河堤坝的横截面,AE=BF,且AE⊥CD,BF⊥CD,垂足分别为E、F,AD=BC,∠C与∠D是否相等?为什么?
如图所示,四边形ABCD是一条河堤坝的横截面,AE=BF,且AE⊥CD,BF⊥CD,垂足分别为E、F,AD=BC,∠C与∠D是否相等?为什么? 如图,∠ACB是一个平角,∠DCE-∠ACD=∠ECF-∠DCE=∠FCG-∠ECF=∠GCB-∠FCG=10°,求∠GCB的度数.
如图,∠ACB是一个平角,∠DCE-∠ACD=∠ECF-∠DCE=∠FCG-∠ECF=∠GCB-∠FCG=10°,求∠GCB的度数. 分别以?ABCD的各边为边,向形外作四个正方形,试说明依次连接这四个正方形对角线的交点所构成的四边形是正方形.
分别以?ABCD的各边为边,向形外作四个正方形,试说明依次连接这四个正方形对角线的交点所构成的四边形是正方形. 如图,在同一平面内,圆O和直线AB相切,P是圆O上一个定点,初始位置圆O和AB相切于点A(此时点P与点A重合),从A处开始圆O在直线AB上以每3分钟1圈的速度匀速向右无滑动地滚动,1分钟到达点E(圆O与AB相切于点E),此时,tan∠PAE的值为$\frac{9}{4π-3\sqrt{3}}$.
如图,在同一平面内,圆O和直线AB相切,P是圆O上一个定点,初始位置圆O和AB相切于点A(此时点P与点A重合),从A处开始圆O在直线AB上以每3分钟1圈的速度匀速向右无滑动地滚动,1分钟到达点E(圆O与AB相切于点E),此时,tan∠PAE的值为$\frac{9}{4π-3\sqrt{3}}$.