题目内容
12．已知a、b、c是三角形的三边长，如果满足（a-6）2+（b-8）4+|c-10|=0，则三角形的形状是直角．分析 先求出a、b、c的值，根据勾股定理的逆定理得出直角三角形即可．
解答 解：∵（a-6）2+（b-8）4+|c-10|=0，
∴a-6=0，b-8=0，c-10=0，
∴a=6，b=8，c=10，
∴a2+b2=c2，
∴三角形是直角三角形，
故答案为：直角．
点评 本题考查了勾股定理的逆定理，绝对值、偶次方的非负性的应用，能灵活运用勾股定理的逆定理进行推理是解此题的关键．
练习册系列答案
相关题目
如图，AE=DB，BC=EF，BC∥EF，求证：△ABC≌△DEF．
如图，在△ABC中，已知BE⊥AC于点E，则以BE为高的三角形是△ABC，△ABE，△BCE．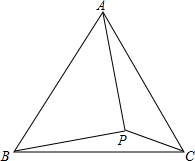
如图，在等边△ABC内有一点P，且PA=2，PB=$\sqrt{3}$，PC=1．
如图，在Rt△ABC中，∠C=90°，M是AB的中点，ME⊥AB交AC于点D，交BC的延长线于点E，求证：CM2=MD•ME．
如图，如果AE∥BF，CE∥DF，那么△OAC∽△OBD吗？为什么？
4．二次函数y=ax2+bx+c满足b2=ac，且x=0时，y=-4，则（ ）
| A． | y最大=-4 | B． | y最小=-4 | C． | y最大=-3 | D． | y最小=-3 |