题目内容
1. O是正方形ABCD的对角线AC的中点,∠EOF的两边交AD,CD于E,F.若∠EOF=90°,求证:AE2+CF2=EF2.
O是正方形ABCD的对角线AC的中点,∠EOF的两边交AD,CD于E,F.若∠EOF=90°,求证:AE2+CF2=EF2.
分析 延长EO交BC于M,连接FM,先证明△AEO≌△CMO,得AE=CM,EO=OM,根据线段垂直平分线的性质得到FE=FM,在RT△CMF中利用勾股定理即可解决.
解答 证明:延长EO交BC于M,连接FM.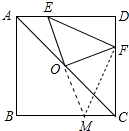
∵四边形ABCD是正方形,
∴AE∥CM,∠BCD=90°
∴∠EAO=∠MCO,
在△AEO和△CMO中,
$\left\{\begin{array}{l}{∠EAO=∠MCO}\\{∠AOE=∠MOC}\\{AO=OC}\end{array}\right.$,
∴△AEO≌△CMO,
∴EO=OM,AE=MC,
∵∠EOF=90°,
∴FO⊥EM,
∴FE=FM,
在RT△ECF中,∵∠MCF=90°,
∴FM2=CM2+CF2,
∵FM=FE,CM=AE,
∴AE2+CF2=EF2.
点评 本题考查正方形的性质、全等三角形的判定和性质、线段垂直平分线性质、勾股定理等知识,解题的关键是添加辅助线,构造全等三角形,属于中考常考题型.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
6.|-9|的相反数是( )
| A. | -9 | B. | 9 | C. | 3 | D. | 没有 |
13.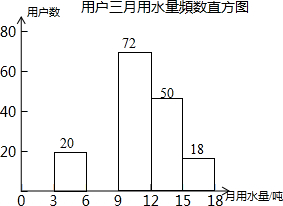 每年5月的第二周为我国城市节约用水宣传周.某社区为了做好今年居民节约用水的宣传,从本社区6000户家庭中随机抽取200户,调查他们家庭今年三月份的用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
每年5月的第二周为我国城市节约用水宣传周.某社区为了做好今年居民节约用水的宣传,从本社区6000户家庭中随机抽取200户,调查他们家庭今年三月份的用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m=40,n=0.25;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费.请估计该社区约有多少户家庭三月份的用水量超过基本月用水量?
 每年5月的第二周为我国城市节约用水宣传周.某社区为了做好今年居民节约用水的宣传,从本社区6000户家庭中随机抽取200户,调查他们家庭今年三月份的用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
每年5月的第二周为我国城市节约用水宣传周.某社区为了做好今年居民节约用水的宣传,从本社区6000户家庭中随机抽取200户,调查他们家庭今年三月份的用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:| 用水量h(吨) | 频数 | 频率 |
| h≤3 | 0 | 0 |
| 3<h≤6 | 20 | 0.10 |
| 6<h≤9 | m | 0.20 |
| 9<h≤12 | 72 | 0.36 |
| 12<h≤15 | 50 | n |
| 15<h≤18 | 18 | 0.09 |
| 18<h | 0 | 0 |
(1)在频数分布表中:m=40,n=0.25;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费.请估计该社区约有多少户家庭三月份的用水量超过基本月用水量?
11.下列各组方程中,属于二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{\frac{x}{3}-\frac{y}{2}=1}\\{3x+6y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{3x+2y=7}\\{xy=5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x+y=1}\\{x+z=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{5}{x}+\frac{y}{3}=\frac{1}{2}}\\{x+2y=3}\end{array}\right.$ |
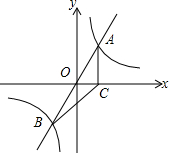 如图,直线y=mx与双曲线y=$\frac{k}{x}$相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.
如图,直线y=mx与双曲线y=$\frac{k}{x}$相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.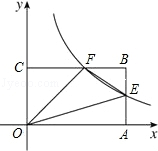 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边长AB、BC分别交于点E、F,已知S△FOC=3 且AE=BE,则:
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边长AB、BC分别交于点E、F,已知S△FOC=3 且AE=BE,则: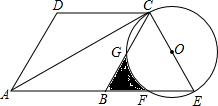 如图:已知菱形ABCD,∠DAB=60°,延长AB到点E,使BE=AB,以CE为直径作⊙O,交BC、BE于点G、F.
如图:已知菱形ABCD,∠DAB=60°,延长AB到点E,使BE=AB,以CE为直径作⊙O,交BC、BE于点G、F.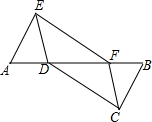 如图,在△AEF中,点D,B分别在边AF和AF的延长线上,已知FB=AD,BC∥AE,且BC=AE,连结CD,CF,DE.
如图,在△AEF中,点D,B分别在边AF和AF的延长线上,已知FB=AD,BC∥AE,且BC=AE,连结CD,CF,DE.