题目内容
16.九年级二班50名同学在“爱心捐款”活动中,捐款情况统计如表,| 捐款金额(元) | 5 | 10 | 15 | 20 | 50 |
| 捐款人数(人) | a | 18 | 10 | 12 | 3 |
(2)二班同学捐款数组成的数据中,中位数是12.5、众数是10;
(3)九年级二班50名同学平均捐款多少元?
(4)根据样本数据,估计该校九年级300名学生在本次活动中捐款多于15元的人数.
分析 (1)用总人数减去其他各组的人数即可求得a的值;
(2)在这组样本数据中,10出现的次数最多,所以求出了众数,将这组样本数据按从小到大的顺序排列,其中处于中间的两个数是10,15,从而求出中位数是12.5;
(3)先根据表格提示的数据求出50名学生的捐款总金额,然后除以50即可求出平均数;
(4)从表格中得知在50名学生中,捐款多于15元的学生有15名,所以可以估计该校九年级300名学生在本次活动中捐款多于15元的人数为300×$\frac{15}{50}$=90.
解答 解:(1)a=50-18-10-12-3=7;
(2)在这组样本数据中,10出现了18次,出现的次数最多,
∴这组样本数据的众数为l0;
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数分别是10,15,
∴这组数据的中位数为l2.5.
(3)观察表格,可知这组样本数据的平均数是=$\frac{5×7+10×18+15×10+20×12+50×3}{50}$=15.1;
∴这组样本数据的平均数是15.1;
(4)在50名学生中,捐款多于15元的学生有15名,有300×$\frac{15}{50}$=90(名).
∴根据样本数据,可以估计该校九年级300名学生在本次活动中捐款多于15元的约有90名.
点评 本题考查了平均数、众数和中位数的定义,用样本估计总体的思想,解题的关键是牢记概念及公式.

练习册系列答案
相关题目
11.若抛物线y=a(x-2)2+a2+a顶点在x轴上,则a的值为( )
| A. | -1 | B. | 0 | C. | 0或-1 | D. | 任意实数 |
1. 如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
 如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )| A. | 120° | B. | 115° | C. | 110° | D. | 105° |
5.下列命题中错误的命题有( )
①线段垂直平分线上的点与这条线段两端距离相等;②若两三角形关于直线L对称,则对应线段所在的直线必相交,且交点在对称轴上;③顶角和底边对应相等的两个等腰三角形全等;④一腰和一腰上的高对应相等的两个等腰三角形全等.
①线段垂直平分线上的点与这条线段两端距离相等;②若两三角形关于直线L对称,则对应线段所在的直线必相交,且交点在对称轴上;③顶角和底边对应相等的两个等腰三角形全等;④一腰和一腰上的高对应相等的两个等腰三角形全等.
| A. | 0个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.当n=1,2,3,4,5,…,2012,2013时,二次函数y=(n2+n)x2-(2n+1)x+1的图象与x轴所截的线段长度之和为( )
| A. | $\frac{2011}{2012}$ | B. | $\frac{2012}{2013}$ | C. | $\frac{2013}{2014}$ | D. | $\frac{2014}{2015}$ |
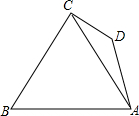 四边形ABCD中,BC⊥CD,∠BCA=60°,∠CDA=135°,BC=10.S△ABC=20$\sqrt{3}$.求AD边的长.
四边形ABCD中,BC⊥CD,∠BCA=60°,∠CDA=135°,BC=10.S△ABC=20$\sqrt{3}$.求AD边的长. 如图,△ABC三边的中线BE,CF相交于点G,若S△ABC=15,则图中阴影部分面积是5.
如图,△ABC三边的中线BE,CF相交于点G,若S△ABC=15,则图中阴影部分面积是5.