题目内容
11.下列说法正确的是( )| A. | 在Rt△ABC中,∠C=90°,若tanA=$\frac{3}{4}$,则a=3,b=4 | |
| B. | 若△ABC三边之比为1:$\sqrt{3}$:$\sqrt{2}$,且∠A为最小角,则sinA=$\frac{1}{2}$ | |
| C. | 对于锐角α,必有sinα>cosα | |
| D. | 在Rt△ABC中,若∠C=90°,则sin2A+cos2A=1 |
分析 根据在直角三角形中,锐角的正切为对边比邻边,可判断A;根据正弦为对边比斜边,可判断B;对于锐角,根据正弦随角的增大而增大,余弦随角的增大而减小,可判断C;根据正弦与余弦的关系,可判断D.
解答 解:A、在Rt△ABC中,∠C=90°,若tanA=$\frac{a}{b}$=$\frac{3}{4}$,则a=3x,b=4x,故A错误;
B、若△ABC三边之比为1:$\sqrt{3}$:$\sqrt{2}$,且∠A为最小角,则sinA=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,故B错误;
C、当α>45°时,sinα>cosα,当0<α<45°时,sinα<cosα,故C错误;
D、在Rt△ABC中,若∠C=90°,则sin2A+cos2A=1,故D正确;
故选:D.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
 如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )| A. | 120° | B. | 115° | C. | 110° | D. | 105° |
2.下列事件中,属于必然事件的是( )
| A. | 随意抛掷一枚骰子,掷得偶数点 | |
| B. | 从一副扑克牌抽出一张,抽得红桃牌 | |
| C. | 任意选择电视的某一频道,正在播放动画片 | |
| D. | 在同一年出生的367名学生中,至少有两个人同月同日生 |
19.下列式子中,正确的是( )
①-|-5|=-5;②|-(-5)|=-5;③-(-5)=-5;④-[-(-5)]=-5.
①-|-5|=-5;②|-(-5)|=-5;③-(-5)=-5;④-[-(-5)]=-5.
| A. | ①和② | B. | ①和③ | C. | ①和④ | D. | ②和③ |
6.当n=1,2,3,4,5,…,2012,2013时,二次函数y=(n2+n)x2-(2n+1)x+1的图象与x轴所截的线段长度之和为( )
| A. | $\frac{2011}{2012}$ | B. | $\frac{2012}{2013}$ | C. | $\frac{2013}{2014}$ | D. | $\frac{2014}{2015}$ |
3.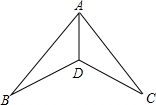 如图,下列条件中,不能证明△ABD≌△ACD的是( )
如图,下列条件中,不能证明△ABD≌△ACD的是( )
 如图,下列条件中,不能证明△ABD≌△ACD的是( )
如图,下列条件中,不能证明△ABD≌△ACD的是( )| A. | ∠B=∠C,BD=DC | B. | BD=DC,AB=AC | C. | ∠B=∠C,∠BAD=∠CAD | D. | ∠ADB=∠ADC,BD=DC |
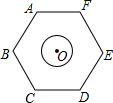 如图,圆心O恰好为正六边形ABCDEF的中心,已知AB=2$\sqrt{3}$,⊙O的半径为1,现将⊙O在正六边形内部沿某一方向平移,当它与正六边形ABCDEF的某条边相切时停止平移,设此时平移的距离为d,则d的取值范围是2≤d≤$\frac{4\sqrt{3}}{3}$.
如图,圆心O恰好为正六边形ABCDEF的中心,已知AB=2$\sqrt{3}$,⊙O的半径为1,现将⊙O在正六边形内部沿某一方向平移,当它与正六边形ABCDEF的某条边相切时停止平移,设此时平移的距离为d,则d的取值范围是2≤d≤$\frac{4\sqrt{3}}{3}$. 如图,C为⊙O的劣弧AB上一点,若∠AOB=124°,则∠ACB=118°.
如图,C为⊙O的劣弧AB上一点,若∠AOB=124°,则∠ACB=118°.