题目内容
已知圆的内接正六边形的周长为36,那么圆的半径为( )
| A、6 | B、4 | C、3 | D、2 |
考点:正多边形和圆
专题:
分析:首先求出∠AOB=
×360°=60°,进而证明△OAB为等边三角形,问题即可解决.
| 1 |
| 6 |
解答: 解:如图,
解:如图,
∵⊙O的内接正六边形ABCDEF的州长为36,
∴边长为6;
∵∠AOB=
×360°=60°,且OA=OB,
∴△OAB为等边三角形,
∴OA=AB=6,
即该圆的半径为6,
故答案为A.
 解:如图,
解:如图,∵⊙O的内接正六边形ABCDEF的州长为36,
∴边长为6;
∵∠AOB=
| 1 |
| 6 |
∴△OAB为等边三角形,
∴OA=AB=6,
即该圆的半径为6,
故答案为A.
点评:该题以正多边形为载体,以正多边形外接圆、正多边形的性质等几何知识点为考查的核心构造而成;灵活运用有关定理来分析、判断、推理或解答是关键.

练习册系列答案
相关题目
 如图,四边形ABCD的两条对角线相交于点P,∠ADB=∠BCA,DC=AP=6,DP=3,则AB=( )
如图,四边形ABCD的两条对角线相交于点P,∠ADB=∠BCA,DC=AP=6,DP=3,则AB=( )| A、15 | B、12 | C、9 | D、6 |
 如图,正十边形A1A2A3A4A5A6A7A8A9A10,连接A7A10,A3A7,则∠A3A7A10的度数为
如图,正十边形A1A2A3A4A5A6A7A8A9A10,连接A7A10,A3A7,则∠A3A7A10的度数为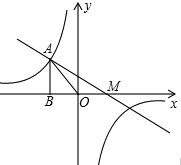 如图,点A(-2,b)是函数y=
如图,点A(-2,b)是函数y=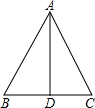 如图,在△ABC中,AB=AC,∠BAD=∠CAD,则下列结论:
如图,在△ABC中,AB=AC,∠BAD=∠CAD,则下列结论: 如图,在Rt△ABC中,∠C=90°,∠B=30°,c=
如图,在Rt△ABC中,∠C=90°,∠B=30°,c=