题目内容
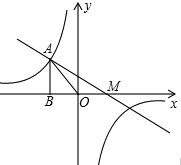 如图,点A(-2,b)是函数y=
如图,点A(-2,b)是函数y=| -4k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:由△AOB的面积为2可求出反比例函数和A点坐标,可求得反比例函数解析式和A点坐标,再代入一次函数解析式可求得一次函数解析式中的a,求得一次函数的解析式,再令y=0可求出M点的坐标,在Rt△ABM中利用勾股定理可求得AM,且容易求得OA,可求得答案.
解答:解:
∵△AOB的面积为2,A(-2,b),
∴
OB•AB=
×2b=2,解得b=2,
∴A点坐标为(-2,2),
∴-4k=-2×2,
解得k=1,
∴反比例函数为y=-
,
又A点在一次函数图象上,
∴2=-2a+1,解得a=-
,
∴一次函数解析式为y=-
x+1,
令y=0,即-
x+1=0,解得x=2,
∴M点坐标为(2,0),
在Rt△ABM中,AB=2,BM=BO+OM=2+2=4,
由勾股定理可得AM=
=
=2
,
且在Rt△AOB中可求得OA=2
,
∴AO:AM=2
:2
=
:
故答案为:
:
.
∵△AOB的面积为2,A(-2,b),
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴A点坐标为(-2,2),
∴-4k=-2×2,
解得k=1,
∴反比例函数为y=-
| 4 |
| x |
又A点在一次函数图象上,
∴2=-2a+1,解得a=-
| 1 |
| 2 |
∴一次函数解析式为y=-
| 1 |
| 2 |
令y=0,即-
| 1 |
| 2 |
∴M点坐标为(2,0),
在Rt△ABM中,AB=2,BM=BO+OM=2+2=4,
由勾股定理可得AM=
| AB2+BM2 |
| 22+42 |
| 5 |
且在Rt△AOB中可求得OA=2
| 2 |
∴AO:AM=2
| 2 |
| 5 |
| 2 |
| 5 |
故答案为:
| 2 |
| 5 |
点评:本题主要考查待定系数法求函数解析式及函数的交点的求法,由三角形的面积求得反比例函数的解析式是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,DE∥BC,
如图,在△ABC中,DE∥BC,| AD |
| BD |
| 1 |
| 2 |
| A、8cm | B、12cm |
| C、11cm | D、10cm |
已知圆的内接正六边形的周长为36,那么圆的半径为( )
| A、6 | B、4 | C、3 | D、2 |
在数轴上与原点的距离等于4的点表示的数是( )
| A、4 | B、-4 |
| C、4或-4 | D、无法确定 |
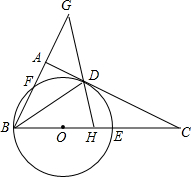 如图,BD为Rt△ABC的角平分线,以BC边上一点O为圆心,过点B、D两点作⊙O,⊙O分别交BC、AB于E、F两点.
如图,BD为Rt△ABC的角平分线,以BC边上一点O为圆心,过点B、D两点作⊙O,⊙O分别交BC、AB于E、F两点. 某校八(4)班每位同学都向汶川地震受灾群众捐款,捐款情况绘制成了扇形统计图,如图所示.求捐款的平均数、众数和中位数.
某校八(4)班每位同学都向汶川地震受灾群众捐款,捐款情况绘制成了扇形统计图,如图所示.求捐款的平均数、众数和中位数.