题目内容
已知圆内接三角形边长为a，求同圆的内接正六边形和外切正方形的边长．
考点：正多边形和圆
专题：
分析：先根据题意画出图形，作直径AB，求出∠CAB=30°，∠ACB=90°，解直角三角形求出AB，即可得出答案．
解答：
解：如图所示，连接AB，则AB过O，连接OD，切AD平分∠A，
∵∠ACB=90°，∠BAC=30°，
∴⊙O的直径=AB=
=
a，
∴⊙O的半径=OA=OD=AD=
AB=
a，
∴同圆的内接六边形的边长为
a；
外切正方形的边长为
a．
解：如图所示，连接AB，则AB过O，连接OD，切AD平分∠A，∵∠ACB=90°，∠BAC=30°，
∴⊙O的直径=AB=
| AC |
| cos30° |
2
| ||
| 3 |
∴⊙O的半径=OA=OD=AD=
| 1 |
| 2 |
| ||
| 3 |
∴同圆的内接六边形的边长为
| ||
| 3 |
外切正方形的边长为
2
| ||
| 3 |
点评：本题考查了圆内接多边形和圆外切多边形的性质，解直角三角形的应用，主要考查学生的计算能力，能求出⊙O的直径是解此题的关键，题目比较好，难度适中．
练习册系列答案
相关题目
如图，已知直线AB与点M，N，求作一点P，使点P在直线AB上，且∠MPA=∠NPB．
如图所示，线段AB=8cm，C为线段AB上一点，又知M是线段BC的中点，N是线段AC的中点，求MN的长．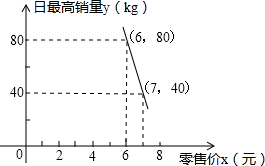
某水果经销商到水果批发市场批发某种水果时了解到如下行情：每千克水果的批发价为4元，经调查，经销商销售该水果的日最高销量与零售价之间的函数关系如图中直线AB所示，该经销商准备购进一定量的水果，且在销售时当日零售价保持不变，考虑到保鲜水果要增加成本，因此经销商要确保每天批发进来的水果全部售完．