��Ŀ����
������С����ͬѧ��ȥ������ɽ���õ��������ݣ�
���³���x(��) | 40 | 80 | 120 | 160 | 200 | 240 |
����ʱ��t(��) | 2 | 5 | 9 | 14 | 20 | 30 |
(1)������120��ʱ������ʱ���Ƕ��٣�
(2)�����ٶ���ʱ���������仯�ģ�
(1)9���ӣ� (2)�����ٶ���ʱ������Ӷ���С�� �����������������(1)�۲������Ϣ��֪����120mʱ,����ʱ��Ϊ9���� (2)����������ͬ�ľ������õ�ʱ�䣬���ɵó�����. ���������(1)�۲������Ϣ��֪����120mʱ,����ʱ��Ϊ9���� (2)��ͼ����֪���³��ȷֱ�Ϊ40m��80mʱ,����ʱ��ֱ�Ϊ2���Ӻ�5���� �ʴ�ʱ����ÿ����10mʱ,����ʱ��Ϊ���� ...��ͼ��ʾ���ó�Ϊ20����˿���ӳ�һ�������Σ��賤���ε�һ��Ϊx�����Ϊy������x�ı仯��y��ֵҲ��֮�仯��
(1)д��y��x֮��Ĺ�ϵʽ����ָ��������仯�У��ĸ����Ա������ĸ����������
(2)�ñ����ʾ��x��1�仯��9ʱ(ÿ������1)��y����Ӧֵ��
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y |
(3)��xΪ��ֵʱ��y��ֵ���
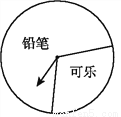
��1��y��10x��x2��x���Ա�����y���������(2)�������������3����xΪ5ʱ��y��ֵ��� �������������������1�������ܳ��ĵ�����ϵ�ɵó����ε���һ��Ϊ10��x����ô�����x(10��x)���Ա�����x��������Ǻ���ֵy�� ��2�������x��ֵ���루1���еĺ�������ʽ��ֵ���ɣ� ��3�����ݣ�2�����õĽ��ۿɵ�xΪ��ֵʱ��y��ֵ��� ��������� �������� ��1����...ij�̳�������һ����������ת����ת��,���涨:�˿���10Ԫ���Ͼ��ܻ��һ��ת��ת�̵Ļ���,��ת��ֹͣʱ,ָ��������һ����Ϳ��Ի����Ӧ�Ľ�Ʒ(��ͼ��ʾ).�±��ǻ�����е�һ��ͳ������:
ת��ת�� �Ĵ���n | 100 | 150 | 200 | 500 | 800 | 1 000 |
���ڡ�Ǧ�ʡ� ����Ĵ���m | 68 | 111 | 136 | 345 | 564 | 701 |
���ڡ�Ǧ�ʡ� �����Ƶ�� |
(1)���㲢��ɱ���.
(2)�����,��n�ܴ�ʱ,���ڡ�Ǧ�ʡ������Ƶ�ʽ���ӽ�����?
(3)������ȥת����ת��һ��,�������ֽ�Ʒ�Ļ����?
(4)�ڸ�ת����,��ʾ��Ǧ�ʡ���������ε�Բ�Ľ�Լ�Ƕ���?
 ��1��0.68��0.74��0.68��0.69��0.705��0.701����2��0.7����3��Ǧ�ʣ���4��252��.
����������������1������Ƶ�ʵ��㷨��Ƶ��=Ƶ�������ɵø���Ƶ�ʣ��ݴ���ռ��ɣ�
��2������3������Ƶ�ʵĶ��壬�ɵõ�n�ܴ�ʱ��Ƶ�ʽ���ӽ�����ʽ��н��
��4����������ͼ�У�ÿ����ռ����İٷֱȵ��ڸò�������Ӧ������Բ�ĽǵĶ�����360��ıȼ��㼴��.
�����...
��1��0.68��0.74��0.68��0.69��0.705��0.701����2��0.7����3��Ǧ�ʣ���4��252��.
����������������1������Ƶ�ʵ��㷨��Ƶ��=Ƶ�������ɵø���Ƶ�ʣ��ݴ���ռ��ɣ�
��2������3������Ƶ�ʵĶ��壬�ɵõ�n�ܴ�ʱ��Ƶ�ʽ���ӽ�����ʽ��н��
��4����������ͼ�У�ÿ����ռ����İٷֱȵ��ڸò�������Ӧ������Բ�ĽǵĶ�����360��ıȼ��㼴��.
�����... ����50�Ŵ�С���ʵؼ�����ͼ������ͬ�ġ����μǡ����│Ƭ,���泯�·�����������,���������ȡһ�Ų����¿�Ƭ����������������ֺ�ԭ���Ż�,ϴ�Ⱥ��ٳ�.ͨ����������,���ֳ鵽���������������│Ƭ��Ƶ��ԼΪ0.3.������Щ��Ƭ�л���������������Ŀ�Ƭ����ԼΪ____.
 15
����������Ϊͨ�����������ֳ鵽���������������│Ƭ��Ƶ��ԼΪ0.3��
���Թ��Ƴ鵽���������������│Ƭ�ĸ���Ϊ0.3��
����Щ��Ƭ�л���������������Ŀ�Ƭ����=0.3��50=15(��).
���Թ�����Щ��Ƭ�л���������������Ŀ�Ƭ����ԼΪ15�š�
�ʴ�Ϊ��15.
15
����������Ϊͨ�����������ֳ鵽���������������│Ƭ��Ƶ��ԼΪ0.3��
���Թ��Ƴ鵽���������������│Ƭ�ĸ���Ϊ0.3��
����Щ��Ƭ�л���������������Ŀ�Ƭ����=0.3��50=15(��).
���Թ�����Щ��Ƭ�л���������������Ŀ�Ƭ����ԼΪ15�š�
�ʴ�Ϊ��15. ��8�֣����A=2x2+3kx��2x��1��B=��x2+kx��1����3A+6B��ֵ��x��ȡֵ�أ���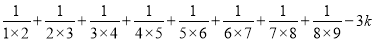 ��ֵ��
��ֵ��
 �������������������A��B����3A+6B����3A+6B��ֵ��x��ȡֵ�ؿ����k��ֵ����k�������ʽ���м��㼴�ɣ�ע������ ��ʽ�ӻ���
��������
3A+6B=3��2x2+3kx��2x��1��+6����x2+kx��1��
=6x 2+9xk-6x-3-6x 2+6xk-6
=15xk-6x-9
=��15k-6��x-9 ,
��3A+6B��ֵ��x��ȡֵ�أ�
��15k=...
�������������������A��B����3A+6B����3A+6B��ֵ��x��ȡֵ�ؿ����k��ֵ����k�������ʽ���м��㼴�ɣ�ע������ ��ʽ�ӻ���
��������
3A+6B=3��2x2+3kx��2x��1��+6����x2+kx��1��
=6x 2+9xk-6x-3-6x 2+6xk-6
=15xk-6x-9
=��15k-6��x-9 ,
��3A+6B��ֵ��x��ȡֵ�أ�
��15k=... �����dz�����Ӣ����ĸ��,Ҳ������ͬλ�ǡ��ڴ��ǡ�ͬ���ڽ�,�����漸����ĸ��,�����ڴ������ٵ���ĸ��(����)
A.  B.
B.  C.
C.  D.
D. 
 C
�������������ڴ��ǵĶ����֪H�к���2���ڴ��ǣ�M�к���2���ڴ��ǣ�N�к���1�ԣ�A�к���2���ڴ���.
��ѡ��C.
C
�������������ڴ��ǵĶ����֪H�к���2���ڴ��ǣ�M�к���2���ڴ��ǣ�N�к���1�ԣ�A�к���2���ڴ���.
��ѡ��C.