题目内容
18.计算:$\sqrt{25}$-$\root{3}{-8}$=7.分析 先依据算术平方根和立方根的性质计算,然后再依据有理数的减法法则计算即可.
解答 解:原式=5-(-2)=7.
故答案为:7.
点评 本题主要考查的是立方根和算术平方根的性质,熟练掌握相关性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.在下列各数中是无理数的有( )
$\frac{1}{3}$,$\sqrt{3}$,$\sqrt{4}$,-π
$\frac{1}{3}$,$\sqrt{3}$,$\sqrt{4}$,-π
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.一元二次方程x2=x的根是( )
| A. | x=1 | B. | x=0 | C. | x1=0,x2=1 | D. | 非以上答案 |
13.(-2)2的算术平方根是( )
| A. | -2 | B. | ±2 | C. | 2 | D. | $\sqrt{2}$ |
10.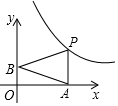 如图,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数y=$\frac{6}{x}$(x>0)图象上,PA⊥x轴,△PAB是以PA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会( )
如图,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数y=$\frac{6}{x}$(x>0)图象上,PA⊥x轴,△PAB是以PA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会( )
 如图,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数y=$\frac{6}{x}$(x>0)图象上,PA⊥x轴,△PAB是以PA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会( )
如图,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数y=$\frac{6}{x}$(x>0)图象上,PA⊥x轴,△PAB是以PA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会( )| A. | 越来越小 | B. | 越来越大 | C. | 不变 | D. | 先变大后变小 |
16.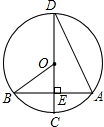 如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )
如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )
 如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )
如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )| A. | $\frac{3}{2}\sqrt{3}$ | B. | $3\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | 3 |
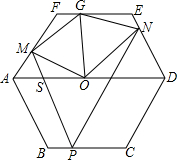 如图,P是正六边形ABCDEF的BC边上的一点,过点P作PM∥AB交AF于M,AD于S,作PN∥CD交DE于N,AD于T,点O是AD的中点,OG平分∠MON,则图中等边三角形有4个.
如图,P是正六边形ABCDEF的BC边上的一点,过点P作PM∥AB交AF于M,AD于S,作PN∥CD交DE于N,AD于T,点O是AD的中点,OG平分∠MON,则图中等边三角形有4个.