题目内容
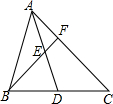 如图,AD是△ABC中BC边上的中线,E为AD的中点,延长BE交AC于点F,AF=
如图,AD是△ABC中BC边上的中线,E为AD的中点,延长BE交AC于点F,AF=| 1 |
| 3 |
| 1 |
| 4 |
考点:平行线分线段成比例,三角形中位线定理
专题:证明题
分析:过D作DQ∥BF交AC于Q,根据平行线分线段成比例定理求出AF=FQ,CQ=FQ,根据三角形的中位线性质得出QD=
BF,EF=
DQ,即可得出答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:
过D作DQ∥BF交AC于Q,
∵E为AD中点,D为BC中点,
∴AF=FQ,CQ=FQ,
∴QD=
BF,EF=
DQ,
∴EF=
BF.

过D作DQ∥BF交AC于Q,
∵E为AD中点,D为BC中点,
∴AF=FQ,CQ=FQ,
∴QD=
| 1 |
| 2 |
| 1 |
| 2 |
∴EF=
| 1 |
| 4 |
点评:本题考查了三角形的中位线定理,平行线分线段成比例定理的应用,解此题的关键是能正确作出辅助线.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
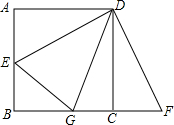 如图,已知正方形ABCD的边长为8,E为AB上一点,点B、C、F在同一条直线上,且AE=CF,当∠EDG为多少度时,存在AE+CG=EG,并证明这个结论.
如图,已知正方形ABCD的边长为8,E为AB上一点,点B、C、F在同一条直线上,且AE=CF,当∠EDG为多少度时,存在AE+CG=EG,并证明这个结论.