题目内容
如图,已知直线l与⊙O相离,OA⊥l于点A,且与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C,设⊙O的半径为r,OA=5.
(1)探究:①求证:AB=AC;②当r=3时,线段AB的长为 ;求出此时线段PB的长;
(2)操作:连接OC,交⊙O于点E,若CB恰好评分∠ACO,判断S△ABE与S△ABC的大小关系,并说明理由.
(3)延伸:若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,直接写出⊙O的半径r的取值范围;
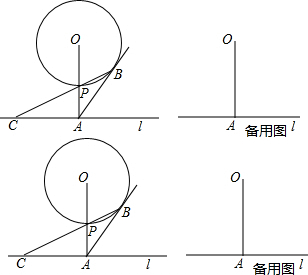
(1)探究:①求证:AB=AC;②当r=3时,线段AB的长为
(2)操作:连接OC,交⊙O于点E,若CB恰好评分∠ACO,判断S△ABE与S△ABC的大小关系,并说明理由.
(3)延伸:若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,直接写出⊙O的半径r的取值范围;

考点:圆的综合题
专题:
分析:(1)①利用切线的性质以及等腰三角形的性质得出∠PCA=∠CBA,即可得出答案;
②利用勾股定理直接求出AB即可,再利用已知得出△OPQ∽△CPA,求出PQ的长;
(2)利用平行线的性质得出CO∥AB即可得出S△ABE与S△ABC的大小关系;
(3)根据题意得出OE=
AC=
AB=
,利用OE=
≤r,
≤2r,求出r得取值范围即可.
②利用勾股定理直接求出AB即可,再利用已知得出△OPQ∽△CPA,求出PQ的长;
(2)利用平行线的性质得出CO∥AB即可得出S△ABE与S△ABC的大小关系;
(3)根据题意得出OE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 52-r2 |
| 1 |
| 2 |
| 52-r2 |
| 25-r2 |
解答:(1)①证明:如图1,连接OB,
∵AB与⊙O相切于点B,
∴OB⊥AB.
∴∠CBA+∠OBP=90°.
∵OA⊥l于点A,
∴∠PCA+∠CPA=90°,
∵OP=OB,
∴∠OBP=∠OPB,
∵∠OPB=∠CPA,
∴∠PCA=∠CBA,
∴AB=AC.
②解:当r=3时,∵AO2=AB2+BO2,
∴AB=
=4,
过点O作OQ⊥PB于点Q,则PB=2PQ,
∵∠OPQ=∠CPA,∠OQP=∠CAP=90°,
∴△OPQ∽△CPA,
∴
=
,
∴
=
,
解得:PQ=
,
∴PB=
;
(2)解:S△ABE=S△ABC;
理由:连接CO,
∵CB平分∠ACO,
∴∠OCP=∠ACP,
∵AB=AC,
∴∠ABC=∠ACP,
∴∠ABC=∠OCP,
∴OC∥AB,
∴S△ABE=S△ABC;
(3)解:如备用图:
作出线段AC的垂直平分线MN,作OE⊥MN,
则可以推出OE=
AC=
AB=
;
又∵圆O与直线MN有交点,
∴OE=
≤r,
≤2r,
25-r2≤4r2,
r2≥5,
∴r≥
,
又∵圆O与直线相离,
∴r<5,
即
≤r<5.
∵AB与⊙O相切于点B,
∴OB⊥AB.
∴∠CBA+∠OBP=90°.
∵OA⊥l于点A,
∴∠PCA+∠CPA=90°,
∵OP=OB,
∴∠OBP=∠OPB,
∵∠OPB=∠CPA,
∴∠PCA=∠CBA,
∴AB=AC.

②解:当r=3时,∵AO2=AB2+BO2,
∴AB=
| 52-32 |
过点O作OQ⊥PB于点Q,则PB=2PQ,
∵∠OPQ=∠CPA,∠OQP=∠CAP=90°,
∴△OPQ∽△CPA,
∴
| OP |
| CP |
| PQ |
| PA |
∴
| 3 | ||
|
| PQ |
| 2 |
解得:PQ=
3
| ||
| 5 |
∴PB=
6
| ||
| 5 |
(2)解:S△ABE=S△ABC;
理由:连接CO,
∵CB平分∠ACO,
∴∠OCP=∠ACP,
∵AB=AC,
∴∠ABC=∠ACP,
∴∠ABC=∠OCP,
∴OC∥AB,
∴S△ABE=S△ABC;

(3)解:如备用图:
作出线段AC的垂直平分线MN,作OE⊥MN,
则可以推出OE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 52-r2 |
又∵圆O与直线MN有交点,
∴OE=
| 1 |
| 2 |
| 52-r2 |
| 25-r2 |
25-r2≤4r2,
r2≥5,
∴r≥
| 5 |
又∵圆O与直线相离,
∴r<5,
即
| 5 |
点评:此题主要考查了圆的综合以及切线的判定与性质和勾股定理以及等腰三角形的性质等知识,得出EO与AB的关系进而求出r取值范围是解题关键.

练习册系列答案
相关题目
 已知:正比例函数y=ax的图象与反比例函数y=
已知:正比例函数y=ax的图象与反比例函数y= 解不等式组
解不等式组