题目内容
6.(猜想规律题)计算:①($\sqrt{2}$+1)($\sqrt{2}$-1)=1;
②($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)=1;
③(2+$\sqrt{3}$)(2-$\sqrt{3}$)=1.
(1)通过以上计算,观察规律,猜想并写出用n(n为正整数)表示上面规律的等式:($\sqrt{n}$+$\sqrt{n-1}$)($\sqrt{n}$-$\sqrt{n-1}$)=n-(n-1)=1
(2)试验证你的猜想.
分析 (1)根据题目所给的运算法则可得规律为:($\sqrt{n}$+$\sqrt{n-1}$)($\sqrt{n}$-$\sqrt{n-1}$)=n-(n-1)=1;
(2)进行二次根式的乘法运算进行计算.
解答 解:(1)①($\sqrt{2}$+1)($\sqrt{2}$-1)=2-1=1;
②($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)=3-2=1;
③(2+$\sqrt{3}$)(2-$\sqrt{3}$)=4-3=1;
规律为:($\sqrt{n}$+$\sqrt{n-1}$)($\sqrt{n}$-$\sqrt{n-1}$)
=n-(n-1)
=1;
(2)($\sqrt{n}$+$\sqrt{n-1}$)($\sqrt{n}$-$\sqrt{n-1}$)
=($\sqrt{n}$)2+$\sqrt{n}•\sqrt{n-1}$-$\sqrt{n}•\sqrt{n-1}$-($\sqrt{n-1}$)2
=n-(n-1)
=1.
故答案为:1;1;1;($\sqrt{n}$+$\sqrt{n-1}$)($\sqrt{n}$-$\sqrt{n-1}$)=n-(n-1)=1.
点评 本题考查了二次根式的混合运算,解答本题的关键是根据题目所给的运算法则得出规律.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
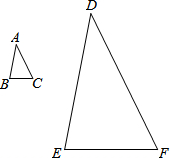 如图,△ABC∽△DEF,AB:DE=1:4,那么,需要16个△ABC才能将△DEF镶嵌满.
如图,△ABC∽△DEF,AB:DE=1:4,那么,需要16个△ABC才能将△DEF镶嵌满.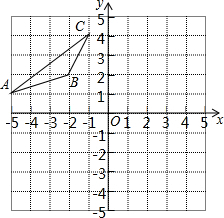 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-5,1),B(-2,2),C(-1,4),请按下列要求画图:
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-5,1),B(-2,2),C(-1,4),请按下列要求画图: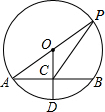 如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点P,连接PC.若AB=8,OC=3,则PC=2$\sqrt{13}$.
如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点P,连接PC.若AB=8,OC=3,则PC=2$\sqrt{13}$.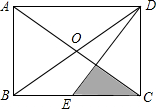 如图,长方形ABCD中,连接BD与AC交于O,E是BC的中点,阴影部分的面积是6平方厘米,求长方形ABCD的面积.
如图,长方形ABCD中,连接BD与AC交于O,E是BC的中点,阴影部分的面积是6平方厘米,求长方形ABCD的面积.