题目内容
如图，AD是△ABC外接圆的直径，AD=6cm，∠DAC=∠ABC，求AC．考点：圆周角定理,相似三角形的判定与性质
专题：
分析：如图，连接DC，证明∠ACD=90°，进而证明AC=AD，根据勾股定理即可解决问题．
解答：
解：如图，连接DC；
∵AD是△ABC外接圆的直径，
∴∠ACD=90°；
又∵∠DAC=∠ABC，
∴AC=AD；
由勾股定理得：AC2+DC2=AD2，
即2AC2=62=36，
∴AC=3
（cm）．
解：如图，连接DC；∵AD是△ABC外接圆的直径，
∴∠ACD=90°；
又∵∠DAC=∠ABC，
∴AC=AD；
由勾股定理得：AC2+DC2=AD2，
即2AC2=62=36，
∴AC=3
| 2 |
点评：该题主要考查了圆周角定理及其推论的应用问题；解题的关键是作辅助线，灵活运用有关定理来分析、判断、或解答．
练习册系列答案
相关题目
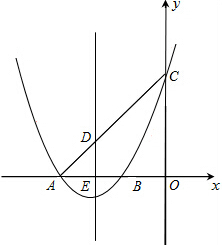已知抛物线y=x2+4x+3交x轴于A、B两点，交y轴于点C，抛物线的对称轴交x轴于点E，求抛物线上是否存在点M，使直线CM把四边形DEOC分成面积相等的两部分？若存在，请写出M所在直线的解析式．
如图，AB、DC、CB分别与⊙O相切于E、F、G，且AB∥CD．
如图，等腰梯形ABCD中，AD∥BC，将其中一条对角线BD平移到CE的位置，则：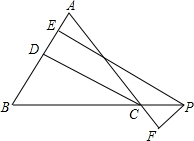
如图，在△ABC中，AB=AC，PE⊥AB，PF⊥AC，CD⊥AB，垂足分别为E、D、F，求证：PE-PF=CD．下列关于角的说法正确的是（ ）
| A、角是由两条射线组成的图形 |
| B、角的边越长，角越大 |
| C、在角一边延长线上取一点 |
| D、角可以看作由一条射线绕着它的端点旋转而形成的图形 |