题目内容
已知,3x2+4y2-12x-8y+16=0,则y2= .
考点:配方法的应用,非负数的性质:偶次方
专题:
分析:将方程的左边重新组合,配成两个非负数的和,借助非负数的性质求出x、y的值即可解决问题.
解答:解:∵3x2+4y2-12x-8y+16=0,
∴3(x2-4x+4)+4(y2-2y+1)=0,
∴3(x-2)2+4(y-1)2=0,
∴x-2=0,y-1=0,
∴x=2,y=1,
∴y2=12=1.
故答案为1.
∴3(x2-4x+4)+4(y2-2y+1)=0,
∴3(x-2)2+4(y-1)2=0,
∴x-2=0,y-1=0,
∴x=2,y=1,
∴y2=12=1.
故答案为1.
点评:本题考查了配方法、非负数的性质及其应用问题;解题的关键是首先将所给方程的左边配成两个非负数和的形式,然后借助非负数的性质求出x、y的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列关于角的说法正确的是( )
| A、角是由两条射线组成的图形 |
| B、角的边越长,角越大 |
| C、在角一边延长线上取一点 |
| D、角可以看作由一条射线绕着它的端点旋转而形成的图形 |
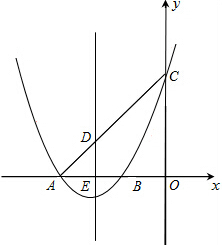 已知抛物线y=x2+4x+3交x轴于A、B两点,交y轴于点C,抛物线的对称轴交x轴于点E,求抛物线上是否存在点M,使直线CM把四边形DEOC分成面积相等的两部分?若存在,请写出M所在直线的解析式.
已知抛物线y=x2+4x+3交x轴于A、B两点,交y轴于点C,抛物线的对称轴交x轴于点E,求抛物线上是否存在点M,使直线CM把四边形DEOC分成面积相等的两部分?若存在,请写出M所在直线的解析式.