题目内容
17.由$({\sqrt{2}+1})({\sqrt{2}-1})=1$,得$\frac{1}{{\sqrt{2}-1}}=\sqrt{2}+1$;由$({\sqrt{3}+\sqrt{2}})({\sqrt{3}-\sqrt{2}})=1$,得$\frac{1}{{\sqrt{3}-\sqrt{2}}}=\sqrt{3}+\sqrt{2}$;
…
观察上面的规律,写出你的发现$\frac{1}{\sqrt{n+1}-\sqrt{n}}$=$\sqrt{n+1}$+$\sqrt{n}$(n≥1).(用含n的式子表示)
分析 根据题中给出的例子找出规律即可得出结论.
解答 解:∵$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}$+1,$\frac{1}{\sqrt{3}-\sqrt{2}}$=$\sqrt{3}$+$\sqrt{2}$,
∴$\frac{1}{\sqrt{n+1}-\sqrt{n}}$=$\sqrt{n+1}$+$\sqrt{n}$(n≥1).
故答案为:$\frac{1}{\sqrt{n+1}-\sqrt{n}}$=$\sqrt{n+1}$+$\sqrt{n}$(n≥1).
点评 本题考查的是分母有理化,熟知分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式是解答此题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
12.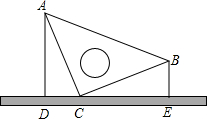 如图,竖直放置一等腰直角三角板,其直角边的长度为10厘米,直角顶点C紧靠在桌面,现量得顶点B到桌面的距离BE=5厘米,则顶点A到桌面的距离AD为( )
如图,竖直放置一等腰直角三角板,其直角边的长度为10厘米,直角顶点C紧靠在桌面,现量得顶点B到桌面的距离BE=5厘米,则顶点A到桌面的距离AD为( )
 如图,竖直放置一等腰直角三角板,其直角边的长度为10厘米,直角顶点C紧靠在桌面,现量得顶点B到桌面的距离BE=5厘米,则顶点A到桌面的距离AD为( )
如图,竖直放置一等腰直角三角板,其直角边的长度为10厘米,直角顶点C紧靠在桌面,现量得顶点B到桌面的距离BE=5厘米,则顶点A到桌面的距离AD为( )| A. | $5\sqrt{3}$厘米 | B. | $5\sqrt{2}$厘米 | C. | 8厘米 | D. | 6厘米 |
4.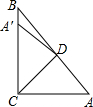 如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠BDA′的度数为( )
如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠BDA′的度数为( )
 如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠BDA′的度数为( )
如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠BDA′的度数为( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
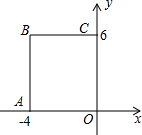 如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,A(-4,0),C(0,6),如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{4}$,那么点B的对应点B′的坐标是(-2,3)或(2,-3).
如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,A(-4,0),C(0,6),如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{4}$,那么点B的对应点B′的坐标是(-2,3)或(2,-3).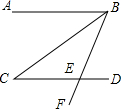 如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠CEF的度数是70°.
如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠CEF的度数是70°.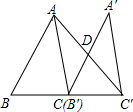 已知:如图,△ABC的面积为12,将△ABC沿BC方向移到△A′B′C′的位置,使B′与C重合,连结AC′交A′C于D,则△C′DC的面积为6.
已知:如图,△ABC的面积为12,将△ABC沿BC方向移到△A′B′C′的位置,使B′与C重合,连结AC′交A′C于D,则△C′DC的面积为6.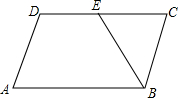 如图,在平行四边形ABCD中,AB=8,AD=5,sinA=$\frac{4}{5}$,E是DC上的一点,且BE=BC,则DE的长为2.
如图,在平行四边形ABCD中,AB=8,AD=5,sinA=$\frac{4}{5}$,E是DC上的一点,且BE=BC,则DE的长为2.