题目内容
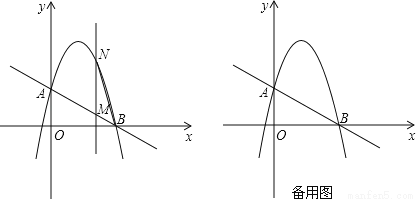
如图,一次函数y=﹣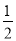 x+2分别交y轴、x轴于A,B两点,抛物线y=﹣x2+bx+c过A,B两点.
x+2分别交y轴、x轴于A,B两点,抛物线y=﹣x2+bx+c过A,B两点.
(1)求这个抛物线的解析式;
(2)作垂直于x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,△NAB的面积有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
练习册系列答案
相关题目
足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
h | 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:

②足球飞行路线的对称轴是直线t= ;
;
③足球被踢出9 s时落地;
④足球被踢出1.5 s时,距离地面的高度是11 m.其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个


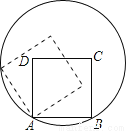
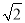 ? B. (
? B. (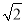 +1)? C. (
+1)? C. (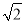 +2)? D. (
+2)? D. (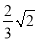 +1)?
+1)?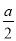 =
=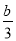 ≠0,求代数式
≠0,求代数式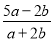 的值;
的值;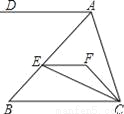
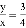 ,则
,则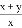 的值为( )
的值为( ) C.
C.  D.
D. 