题目内容
3.列方程(组)解应用题为改善办学条件,某中学计划购买A品牌电脑和B品牌课桌,第一次,用9万元购买了A品牌电脑10台和B品牌课桌200张,第二次,用9万元购买了A品牌电脑12台和B品牌课桌120张.
(1)每台A品牌电脑与每张B品牌课桌的价格各是多少元?
(2)第三次购买时,销售商对一次购买量大的客户打折销售,规定:一次购买A品牌电脑35台以上(含35台),按九折销售;一次购买B品牌课桌600张以上(含600张),按八折销售,学校准备用27万元整购买电脑和课桌,其中电脑不少于35台,课桌不少于600张,有哪几种购买方案?
分析 (1)设每台A品牌电脑m元,每张B品牌课桌n元,列方程组即可求解;
(2)设购电脑x台,课桌y张,列出方程组,解得x、y的取值范围,再确定购买方案.
解答 解:(1)设每台A品牌电脑m元,每张B品牌课桌n元,
则有$\left\{\begin{array}{l}{10m+200n=90000}\\{12m+120n=90000}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=6000}\\{n=150}\end{array}\right.$.
答:每台A品牌电脑6000元,每张B品牌课桌150元.
(2)有两种方案.设购电脑x台,则课桌有$\frac{270000-5400x}{120}$张,
则有$\left\{\begin{array}{l}{x≥35}\\{\frac{270000-5400x}{120}≥600}\end{array}\right.$
解得:35≤x≤36$\frac{2}{3}$,
则x=35或36.
x=35时,$\frac{270000-5400x}{120}$=675(张);
x=36时,$\frac{270000-5400x}{120}$=630(张).
方案①:购电脑35台,课桌675张;
方案②:购电脑36台,课桌630张.
点评 本题考查了二元一次方程组的应用,需要找到两个等量关系式是关键;还考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式实关键.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
4. 如图,梯形ABCD中,AB∥CD,∠D=( )
如图,梯形ABCD中,AB∥CD,∠D=( )
 如图,梯形ABCD中,AB∥CD,∠D=( )
如图,梯形ABCD中,AB∥CD,∠D=( )| A. | 120° | B. | 135° | C. | 145° | D. | 155° |
13.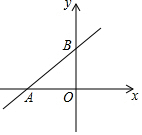 如图,直线y=kx+b与x轴、y轴分别相交于点A(-3,0)、B(0,2),则不等式kx+b>0的解集是( )
如图,直线y=kx+b与x轴、y轴分别相交于点A(-3,0)、B(0,2),则不等式kx+b>0的解集是( )
 如图,直线y=kx+b与x轴、y轴分别相交于点A(-3,0)、B(0,2),则不等式kx+b>0的解集是( )
如图,直线y=kx+b与x轴、y轴分别相交于点A(-3,0)、B(0,2),则不等式kx+b>0的解集是( )| A. | x>-3 | B. | x<-3 | C. | x>2 | D. | x<2 |
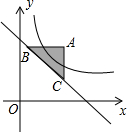 如图,在平面直角坐标系中,过点A(4,5)分别作x轴、y轴的平行线,交直线y=-x+6于B、C两点.若函数y=$\frac{k}{x}$(x>0)的图象与△ABC的边有公共点,则k的取值范围是5≤k≤20.
如图,在平面直角坐标系中,过点A(4,5)分别作x轴、y轴的平行线,交直线y=-x+6于B、C两点.若函数y=$\frac{k}{x}$(x>0)的图象与△ABC的边有公共点,则k的取值范围是5≤k≤20.
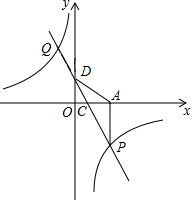 如图,一次函数y=kx+1图象与反比例函数y=$\frac{m}{x}$的图象交于P、Q两点,过点P作PA⊥x轴,一次函数图象分别交x轴、y轴于C、D两点,$\frac{CD}{CP}$=$\frac{1}{3}$,且A(4,0).
如图,一次函数y=kx+1图象与反比例函数y=$\frac{m}{x}$的图象交于P、Q两点,过点P作PA⊥x轴,一次函数图象分别交x轴、y轴于C、D两点,$\frac{CD}{CP}$=$\frac{1}{3}$,且A(4,0).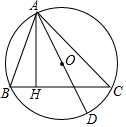 如图,AD是△ABC的外接圆O的直径,AH⊥BC于H.
如图,AD是△ABC的外接圆O的直径,AH⊥BC于H.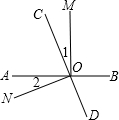 如图,直线AB、CD相交于点O,OM⊥AB.
如图,直线AB、CD相交于点O,OM⊥AB.