题目内容
14.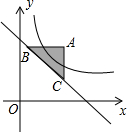 如图,在平面直角坐标系中,过点A(4,5)分别作x轴、y轴的平行线,交直线y=-x+6于B、C两点.若函数y=$\frac{k}{x}$(x>0)的图象与△ABC的边有公共点,则k的取值范围是5≤k≤20.
如图,在平面直角坐标系中,过点A(4,5)分别作x轴、y轴的平行线,交直线y=-x+6于B、C两点.若函数y=$\frac{k}{x}$(x>0)的图象与△ABC的边有公共点,则k的取值范围是5≤k≤20.
分析 根据题意可以分别求得点B、点C的坐标,从而可以得到k的取值范围,本题得以解决.
解答 解:∵过点A(4,5)分别作x轴、y轴的平行线,交直线y=-x+6于B、C两点,
∴点B的纵坐标为5,点C的横坐标为4,
将y=5代入y=-x+6,得x=1;
将x=4代入y=-x+6得,y=2,
∴点B的坐标为(1,5),点C的坐标为(4,2),
∵函数y=$\frac{k}{x}$(x>0)的图象与△ABC的边有公共点,点A(4,5),点B(1,5),
∴1×5≤k≤4×5
即5≤k≤20,
故答案为:5≤k≤20.
点评 本题考查反比例函数与一次函数的交点问题,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
16. 如图是某个几何体的展开图,该几何体是( )
如图是某个几何体的展开图,该几何体是( )
 如图是某个几何体的展开图,该几何体是( )
如图是某个几何体的展开图,该几何体是( )| A. | 三棱柱 | B. | 圆锥 | C. | 四棱柱 | D. | 圆柱 |
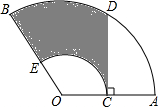 如图,在扇形OAB中,C是OA的中点,CD⊥OA,CD与$\widehat{AB}$交于点D,以O为圆心,OC的长为半径作$\widehat{CE}$交OB于点E,若OA=4,∠AOB=120°,则图中阴影部分的面积为$\frac{4}{3}$π+2$\sqrt{3}$.(结果保留π)
如图,在扇形OAB中,C是OA的中点,CD⊥OA,CD与$\widehat{AB}$交于点D,以O为圆心,OC的长为半径作$\widehat{CE}$交OB于点E,若OA=4,∠AOB=120°,则图中阴影部分的面积为$\frac{4}{3}$π+2$\sqrt{3}$.(结果保留π)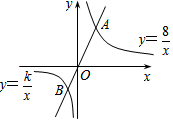 如图,点A为反比例函数y=$\frac{8}{x}$(x>0)图象上一点,点B为反比例函数y=$\frac{k}{x}$
如图,点A为反比例函数y=$\frac{8}{x}$(x>0)图象上一点,点B为反比例函数y=$\frac{k}{x}$