题目内容
12.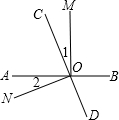 如图,直线AB、CD相交于点O,OM⊥AB.
如图,直线AB、CD相交于点O,OM⊥AB.(1)若∠1=∠2,证明:ON⊥CD;
(2)若∠1=$\frac{1}{4}$∠BOC,求∠BOD的度数.
分析 (1)利用垂直的定义得出∠2+∠AOC=90°,进而得出答案;
(2)根据题意得出∠1的度数,即可得出∠BOD的度数.
解答 (1)证明:∵OM⊥AB,
∴∠AOM=∠BOM=90°,
∴∠1+∠AOC=90°,
∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠CON=90°,
∴ON⊥CD;
(2)解:∵∠1=$\frac{1}{4}$∠BOC,
∴∠BOM=3∠1=90°,
解得:∠1=30°,
∴∠BOD=90°-30°=60°.
点评 此题主要考查了垂直的定义以及邻补角、对顶角等知识,正确把握垂直的定义是解题关键.

练习册系列答案
相关题目
17.如果关于x的方程x2+4x-m=0没有实数根,则m的取值范围是( )
| A. | m<-4 | B. | m>-4 | C. | m≤-4 | D. | m≥-4 |
4.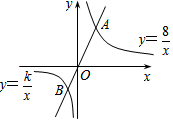 如图,点A为反比例函数y=$\frac{8}{x}$(x>0)图象上一点,点B为反比例函数y=$\frac{k}{x}$
如图,点A为反比例函数y=$\frac{8}{x}$(x>0)图象上一点,点B为反比例函数y=$\frac{k}{x}$
(x<0)图象上一点,直线AB过原点O,且OA=2OB,则k的值为( )
 如图,点A为反比例函数y=$\frac{8}{x}$(x>0)图象上一点,点B为反比例函数y=$\frac{k}{x}$
如图,点A为反比例函数y=$\frac{8}{x}$(x>0)图象上一点,点B为反比例函数y=$\frac{k}{x}$(x<0)图象上一点,直线AB过原点O,且OA=2OB,则k的值为( )
| A. | 2 | B. | 4 | C. | -2 | D. | -4 |
1.不等式组$\left\{\begin{array}{l}{x+1>0}\\{x-3>0}\end{array}\right.$的解是( )
| A. | x>-1 | B. | x>3 | C. | -1<x<3 | D. | x<3 |
2.如图,在下图中有对顶角的图形是( )


| A. | ① | B. | ①② | C. | ②④ | D. | ②③ |