题目内容
7.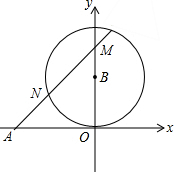 如图,已知A(-2,0),以B(0,1)为圆心,OB长为半径作⊙B,N是⊙B上一个动点,直线AN交y轴于M点,则△AOM面积的最大值是( )
如图,已知A(-2,0),以B(0,1)为圆心,OB长为半径作⊙B,N是⊙B上一个动点,直线AN交y轴于M点,则△AOM面积的最大值是( )| A. | 2 | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{16}{3}$ |
分析 当直线AN与⊙B相切时,△AOM面积的最大.设BM=x,由切割线定理表示出MN,可证明△BNM∽△AOM,根据相似三角形的性质可求得x,然后求得△AOM面积.
解答 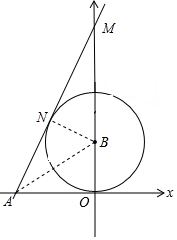 解:当直线AN与⊙B相切时,△AOM面积的最大.
解:当直线AN与⊙B相切时,△AOM面积的最大.
连接AB、BN,
在Rt△AOB和Rt△ANB中
$\left\{\begin{array}{l}{OB=BN}\\{AB=AB}\end{array}\right.$
∴Rt△AOB≌Rt△ANB,
∴AN=AO=2,
设BM=x,
∴MN2=(BM-1)(BM+1),
∴MN=$\sqrt{{x}^{2}-1}$,
∵∠AOM=∠BNM=90°,∠AMO=∠BMN,
∴△BNM∽△AOM,
∴$\frac{BN}{OA}$=$\frac{MN}{OM}$,
即$\frac{1}{2}$=$\frac{\sqrt{{x}^{2}-1}}{x+1}$,
解得x=$\frac{5}{3}$,
S△AOM=$\frac{OA•OM}{2}$=$\frac{2×(\frac{5}{3}+1)}{2}$=$\frac{8}{3}$.
故选:B.
点评 本题是一个动点问题,考查了切线的性质和三角形面积的计算,解题的关键是确定当射线AN与⊙B相切时,△AOM面积的最大.

练习册系列答案
相关题目
10. 如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,AC的长为半径作弧交数轴于点M,则点M表示的数为( )
如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,AC的长为半径作弧交数轴于点M,则点M表示的数为( )
 如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,AC的长为半径作弧交数轴于点M,则点M表示的数为( )
如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,AC的长为半径作弧交数轴于点M,则点M表示的数为( )| A. | $\sqrt{10}$-1 | B. | $\sqrt{5}$-1 | C. | 2 | D. | $\sqrt{5}$ |
11.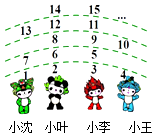 如图四个小朋友站成一排,老师按图中所示的规则数数,数到2016时对应的小朋友可得一朵红花.那么,得红花的小朋友是( )
如图四个小朋友站成一排,老师按图中所示的规则数数,数到2016时对应的小朋友可得一朵红花.那么,得红花的小朋友是( )
 如图四个小朋友站成一排,老师按图中所示的规则数数,数到2016时对应的小朋友可得一朵红花.那么,得红花的小朋友是( )
如图四个小朋友站成一排,老师按图中所示的规则数数,数到2016时对应的小朋友可得一朵红花.那么,得红花的小朋友是( )| A. | 小沈 | B. | 小叶 | C. | 小李 | D. | 小王 |
19.以下条件不可以判定△ABC与△A′B′C′相似的是( )
| A. | $\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$=$\frac{BC}{B′C′}$ | B. | $\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,且∠A=∠A’ | ||
| C. | ∠A=∠B’,∠B=∠C’ | D. | $\frac{AC}{A′C′}$=$\frac{BC}{B′C′}$,且∠A=∠A’ |
17.若x=$\root{3}{-2}$,则下列式子正确的是( )
| A. | 3x=-2 | B. | x3=-2 | C. | (-x)3=-2 | D. | x=(-2)3 |
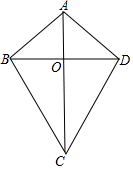 定义:有两组邻边相等的四边形是筝形
定义:有两组邻边相等的四边形是筝形