题目内容
12．已知方程x2+6x+k=0有两个相等的实数根，则k=9．分析 由方程有两个相等的实数根，得到根的判别式等于0，列出关于k的方程，求出方程的解即可得到k的值．
解答 解：∵方程x2+6x+k=0有两个相等的实数根，
∴△=b2-4ac=36-4k=0，
解得：k=9．
故答案为：9．
点评 此题考查了一元二次方程根的判别式，当根的判别式的值大于0，一元二次方程有两个不相等的实数根；当根的判别式等于0，一元二次方程有两个相等的实数根；当根的判别式小于0，一元二次方程没有实数根．
练习册系列答案
相关题目
16．下列式子正确的是（ ）
| A． | a-2（-b+c）=a+2b-2c | B． | |-a|=-|a| | C． | a3+a3=2a6 | D． | 6x2-2x2=4 |
7．
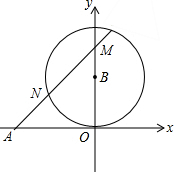如图，已知A（-2，0），以B（0，1）为圆心，OB长为半径作⊙B，N是⊙B上一个动点，直线AN交y轴于M点，则△AOM面积的最大值是（ ）
如图，已知A（-2，0），以B（0，1）为圆心，OB长为半径作⊙B，N是⊙B上一个动点，直线AN交y轴于M点，则△AOM面积的最大值是（ ）| A． | 2 | B． | $\frac{8}{3}$ | C． | 4 | D． | $\frac{16}{3}$ |
17．在$\sqrt{2}$，-$\sqrt{3}$，1，0这四个数中，最小的一个数是（ ）
| A． | $\sqrt{2}$ | B． | -$\sqrt{3}$ | C． | 1 | D． | 0 |
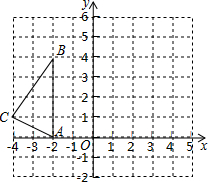如图，在坐标系中，△ABC三顶点坐标为A（-2，0），B（-2，4），C（-4，1），将△ABC绕着P点顺时针旋转90°后得到△A1B1C1，其中A点对应点A1的坐标为（1，3），C点对应点C1的坐标为（2，5）．