题目内容
1.某饰品店以20元/件的价格采购了一批今年新上市的饰品进行了为期30天的销售,销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系:P=-2x+80(1≤x≤30);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:Q1=$\frac{1}{2}$x+30(1≤x≤20),后10天的销售价格Q2则稳定在45元/件.(1)试分别写出该商店前20天的日销售利润R1(元)和后10天的日销售利润R2(元)与销售时间x(天)之间的函数关系式;
(2)请问在这30天的销售期中,哪一天的日销售利润最大?并求出这个最大利润值.
(注:销售利润=销售收入-购进成本)
分析 (1)根据题意可以分表示出该商店前20天的日销售利润R1(元)和后10天的日销售利润R2(元)与销售时间x(天)之间的函数关系式;
(2)有第一问中的函数关系式可以分别求出在各自范围内的最大值,然后进行比较即可解答本题.
解答 解:(1)由题意可得,
R1=P(Q1-20)=(-2x+80)[($\frac{1}{2}$x+30)-20]=-x2+20x+800,
R2=P(Q2-20)=(-2x+80)(45-20)=-50x+2000,
即该商店前20天的日销售利润R1(元)和后10天的日销售利润R2(元)与销售时间x(天)之间的函数关系式分别是:${R}_{1}=-{x}^{2}+20x+800,{R}_{2}=-50x+2000$;
(2)∵当1≤x≤20时,R1=-(x-10)2+900,
∴当x=10时,R1的最大值为900,
当21≤x≤30时,R2=-50x+2000,
∵R2的值随x值的增大而减小,∴当x=21时,R2的最大值是950,
∵950>900,
∴在第21天时,日销售利润最大,最大利润为950元.
点评 本题考查二次函数的应用,解题的关键是明确题意可以列出相应的函数关系式,并可以求函数的最值.

练习册系列答案
相关题目
16.在平面直角坐标系中,若点P(a-1,a)在第二象限,则a的取值范围是( )
| A. | a<0 | B. | a>1 | C. | 0<a<1 | D. | -1<a<0 |
13.二次函数y=(x-1)2+2的最小值是( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
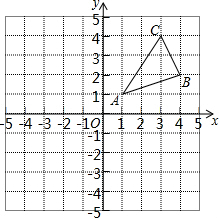 如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).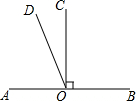 如图,已知直线AB,线段CO⊥AB于O,∠AOD=$\frac{1}{2}$∠BOD,求∠COD的度数.
如图,已知直线AB,线段CO⊥AB于O,∠AOD=$\frac{1}{2}$∠BOD,求∠COD的度数. 已知:如图,A,O,B三点在同一条直线上,∠A=∠C,∠1=∠2,OD=OB.求证:AD=CB.
已知:如图,A,O,B三点在同一条直线上,∠A=∠C,∠1=∠2,OD=OB.求证:AD=CB. 已知抛物线的顶点为(0,4)且与x轴交于(-2,0),(2,0).
已知抛物线的顶点为(0,4)且与x轴交于(-2,0),(2,0).