Question

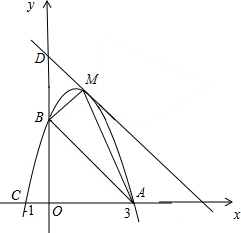
如图：
（1）分别求出直线和抛物线的解析式；
（2）若M为抛物线第一象限的动点，求S_△AMB的最值．

Answer 1

考点：待定系数法求二次函数解析式,待定系数法求一次函数解析式,二次函数图象上点的坐标特征

专题：

分析：（1）由图可得点A，C，B的坐标，设抛物线的解析式为y=ax²+bx+c，把A（3，0），B（-1，0），C（0，3）代入得出方程组，求解即可得出抛物线的解析式，设直线AB的解析式为y=kx+b，把A（3，0），B（0，3）代入可得方程组，求解即可得出直线的解析式，
（2）当直线平行与直线AB，且与抛物线只有一个交点时，S_△AMB的最值．设直线为y=-x+b，可得-x+b=-x²+2x+3，利用△=0解得b的值，利用图形可得出BD的值，再由∠ODM=45°，BM⊥DM，可得BM的值，利用三角形面积公式即可求出S_△AMB．

解答：解：（1）由图可得A（3，0），C（-1，0），B（0，3），
设抛物线的解析式为y=ax²+bx+c，
把A（3，0），B（-1，0），C（0，3）代入可得

9a+3b+c=0 a-b+c=0 c=3

，解得

a=-1 b=2 c=3

，
所以抛物线的解析式为y=-x²+2x+3，
设直线AB的解析式为y=kx+b，
把A（3，0），B（0，3）代入得

3k+b=0 b=3

，解得

k=-1 b=3

，
所以y=-x+3，
（2）当直线平行与直线AB，且与抛物线只有一个交点时，S_△AMB的最值．
设直线为y=-x+b，
可得-x+b=-x²+2x+3，化简得，x²-3x+b-3=0，
由△=0可得9-4×（b-3）=0，解得b=

21

4

，
如图，BD=b-OB=

21

4

-3=

9

4

，

∵∠ODM=45°，
∴BM⊥DM，
∴BM=

9 2

8

，
∴S_△AMB=

1

2

×3

2

×

9 2

8

=

27

8

．

点评：本题主要考查了用待定系数法求二次函数及一次函数，图象上坐标点的特征等，解题的关键是利用△求出b的值．