题目内容
已知部分锐角三角函数值:sin15°=
,sin30°=
,sin45°=
,sin75°=
,计算cos75°= .(提示:sin2x+cos2x=1)
| ||||
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| ||||
| 4 |
考点:互余两角三角函数的关系,特殊角的三角函数值
专题:
分析:根据互余两角三角函数的关系:cosA=sin(90°-∠A)即可求解.
解答:解:∵sin15°=
,
∴cos75°=sin(90°-75°)=sin15°=
.
故答案为
.
| ||||
| 4 |
∴cos75°=sin(90°-75°)=sin15°=
| ||||
| 4 |
故答案为
| ||||
| 4 |
点评:本题考查了互余两角三角函数的关系:在直角三角形中,∠A+∠B=90°时,正余弦之间的关系为:
①一个角的正弦值等于这个角的余角的余弦值,即sinA=(90°-∠A);
②一个角的余弦值等于这个角的余角的正弦值,即cosA=sin(90°-∠A);
也可以理解成若∠A+∠B=90°,那么sinA=cosB或sinB=cosA.
①一个角的正弦值等于这个角的余角的余弦值,即sinA=(90°-∠A);
②一个角的余弦值等于这个角的余角的正弦值,即cosA=sin(90°-∠A);
也可以理解成若∠A+∠B=90°,那么sinA=cosB或sinB=cosA.

练习册系列答案
相关题目
已知点P(-4,a)关于x轴的对称点P′在第二象限,则a可能为( )
| A、-3 | B、1 | C、2 | D、3 |
 如图:
如图: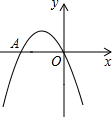 如图,二次函数y=x2+bx+c的图象经过坐标原点,且与x轴交于A(-2,0).
如图,二次函数y=x2+bx+c的图象经过坐标原点,且与x轴交于A(-2,0). 如图,小明为了测量小山顶的塔高,他在A处测得塔尖D的仰角为45°,再沿AC方向前进73.2m到达山脚B处,测得塔尖D的仰角为60°,山坡BE的坡度i=1:
如图,小明为了测量小山顶的塔高,他在A处测得塔尖D的仰角为45°,再沿AC方向前进73.2m到达山脚B处,测得塔尖D的仰角为60°,山坡BE的坡度i=1: