题目内容
19.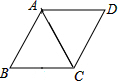 如图,已知菱形ABCD中,AC是对角线,∠B=60°.
如图,已知菱形ABCD中,AC是对角线,∠B=60°.(1)求作:△ABC的外接圆⊙O(要求:用直尺和圆规作图,不写作法,保留作图痕迹)
(2)判断AD所在直线与⊙O的位置关系,并说明理由.
分析 (1)分别作AB和BC的垂直平分线,两垂直平分线相交于点O,然后以O为圆心,OA为半径作圆即可;
(2)由菱形的性质得AB=BC,∠B=60°,则可判断△ABC为等边三角形,于是得到点O为△BAC的内心,连接AO并延长AO交BC于点E,如图2,则AE平分∠BAC,根据等边三角形的性质得AE⊥BC,所以AE⊥AD,
然后根据切线的判定定理得到AD为⊙O的切线.
解答 解:(1)如图1,⊙O为所求作的圆.
(2)AD为⊙O的切线.理由如下:
∵四边形ABCD为菱形,
∴AB=BC,∠B=60°,
∴△ABC为等边三角形,
∴点O为△BAC的内心,
连接AO并延长AO交BC于点E,如图2,
∵AE平分∠BAC,
∴AE⊥BC,
∵AD∥BC,
∴AE⊥AD,
∴AD为⊙O的切线.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了三角形的外心、菱形的性质和切线的判定.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
9. 如图,在4×4的正方形网格中,则tanα的值是( )
如图,在4×4的正方形网格中,则tanα的值是( )
 如图,在4×4的正方形网格中,则tanα的值是( )
如图,在4×4的正方形网格中,则tanα的值是( )| A. | 1 | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
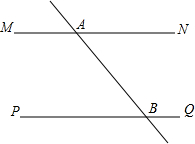 如图,公路MN∥PQ,公路AB交公路MN于A,交公路PQ于B,若要建一汽车旅店到三条公路的距离相等,则可供选择的地址有( )
如图,公路MN∥PQ,公路AB交公路MN于A,交公路PQ于B,若要建一汽车旅店到三条公路的距离相等,则可供选择的地址有( )
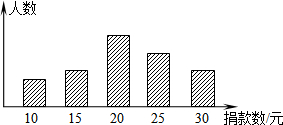 振兴中学某班学生对本校学生会倡导的“助学”捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:8:6:4,又知此次调查中捐款20元和25元的学生共28人.
振兴中学某班学生对本校学生会倡导的“助学”捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:8:6:4,又知此次调查中捐款20元和25元的学生共28人. 如图,四边形ABCD是平行四边形,点E为DC延长线上一点,联接AE,交边BC于点F,联接BE.求证:AB•AD=BF•ED.
如图,四边形ABCD是平行四边形,点E为DC延长线上一点,联接AE,交边BC于点F,联接BE.求证:AB•AD=BF•ED.