题目内容
17.计算(1)(-6)+(+8)-(+4)-(-2)
(2)(-7)×(-5)-90÷(-15)
(3)($\frac{1}{2}$-$\frac{5}{9}$+$\frac{7}{12}$)×(-36)
(4)2÷(-$\frac{3}{7}$)×$\frac{4}{7}$÷(-$\frac{8}{3}$)
(5)-24+(4-9)2-5×(-1)6
(6)用简便方法计算:(-370)×(-$\frac{1}{4}$)+0.25×24.5-5$\frac{1}{2}$×(-25%)
分析 (1)原式利用减法法则变形,计算即可得到结果;
(2)原式先计算乘除运算,再计算加减运算即可得到结果;
(3)原式利用乘法分配律计算即可得到结果;
(4)原式从左到右依次计算即可得到结果;
(5)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果;
(6)原式变形后,逆用乘法分配律计算即可得到结果.
解答 解:(1)原式=-6+8-4+2=-10+10=0;
(2)原式=25+6=31;
(3)原式=-18+20-21=-19;
(4)原式=2×$\frac{7}{3}$×$\frac{4}{7}$×$\frac{3}{8}$=1;
(5)原式=-16+25-5=4;
(6)原式=0.25×(370+24.5+5.5)=0.25×400=100.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
7.下列各式中,能用平方差公因式分解的是( )
| A. | x2+x | B. | x2+8x+16 | C. | x2+4 | D. | x2-1 |
12.近似数2.60所表示的精确值x的取值范围( )
| A. | 2.600<x≤2.605 | B. | 2.595<x≤2.605 | C. | 2.595≤x<2.605 | D. | 2.50≤x<2.70 |
6.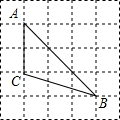 如图,方格中的每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上,则sinB的值为( )
如图,方格中的每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上,则sinB的值为( )
 如图,方格中的每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上,则sinB的值为( )
如图,方格中的每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上,则sinB的值为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{5}}{3}$ | D. | $\frac{\sqrt{5}}{5}$ |
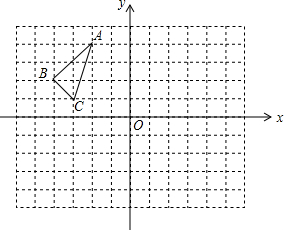 如图所示,把△ABC置于平面直角坐标系中,请你按下列要求分别画图:
如图所示,把△ABC置于平面直角坐标系中,请你按下列要求分别画图: 如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).(结果保留根号)
如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).(结果保留根号)