题目内容
17.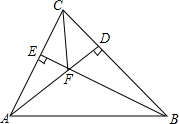 如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,AD、BE相交于点F,连接CF.
如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,AD、BE相交于点F,连接CF.(1)在△ABC中,AC边上的高为BE,BC边上的高为AD;
(2)在△ABD中,AD边上的高为BD;
(3)在△BCE中,CE边上的高为BE;
(4)在△BCF中,BC边上的高为FD;
(5)在△ABF中,AF边上的高为BD,BF边上的高为AE.
分析 三角形的高即从三角形的一个顶点向它的对边引垂线,顶点和垂足间的线段.根据概念可求解各小题.
解答 解:(1)在△ABC中,AC边上的高为BE,BC边上的高为AD;
(2)在△ABD中,AD边上的高为BD;
(3)在△BCE中,CE边上的高为BE;
(4)在△BCF中,BC边上的高为FD;
(5)在△ABF中,AF边上的高为BD,BF边上的高为AE.
故答案为BE,AD;BD;BE;FD;BD,AE.
点评 本题考查了三角形的高,由定义可知,三角形的高是线段,线段的两个端点一个是三角形的顶点,另一个是垂足.注意:锐角三角形的三条高在三角形内部,相交于三角形内一点;直角三角形有两条高与直角边重合,另一条高在三角形内部,它们的交点是直角顶点;钝角三角形有两条高在三角形外部,一条高在三角形内部,三条高所在直线相交于三角形外一点.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
7.若两圆的半径分别为2和4,圆心距为4,则两圆的位置关系为 ( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
8.用配方法解方程x2+10x+20=0,则方程可变形为( )
| A. | (x+5)2 | B. | (x-5)2=45 | C. | (x+5)2=5 | D. | (x-5)2=5 |
2.方程x2+px+q=0的两个根中,有一个且只有一个为0,则p、q应满足( )
| A. | p=0,q=0 | B. | p=0,q≠0 | C. | p≠0,q=0 | D. | p≠0,q≠0 |
 已知:如图,∠BGF=140°,求∠A+∠B+∠C+∠D+∠E+∠F的度数?
已知:如图,∠BGF=140°,求∠A+∠B+∠C+∠D+∠E+∠F的度数?