题目内容
7.一个长方体盒子,长6cm,宽3cm,高4cm.要把一根木棒放进盒子里.设木棒的最大长度为a cm.(1)求a2的值;
(2)估计a的值(结果精确到0.1)
分析 (1)木棒的最大长度是长方体的对角线的长度,根据长方体的性质构造出直角三角形,利用勾股定理解答即可.
(2)对(1)中的a2开平方,进行估算.
解答  解:(1)连接BD,BH.
解:(1)连接BD,BH.
在Rt△ABD中,AB=6cm,AB=3cm,
由勾股定理得:BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$(cm).
又∵在Rt△BDH中,DH=4cm,
∴由勾股定理得:BH2=DH2+BD2=32+45=54,即a2=54;
(2)由(1)知,a2=54.则a=$\sqrt{54}$=3$\sqrt{6}$≈7.4.
点评 本题考查正确运用勾股定理及正方体的性质,善于观察题目的信息是解题以及学好数学的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
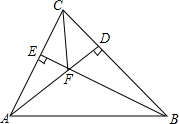 如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,AD、BE相交于点F,连接CF.
如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,AD、BE相交于点F,连接CF. 如图,在△ABC中,点D在AB的延长线上,若∠A=60°,∠C=50°,∠CBD=110°;若∠C=40°,∠CBD=105°,则∠A=65°.
如图,在△ABC中,点D在AB的延长线上,若∠A=60°,∠C=50°,∠CBD=110°;若∠C=40°,∠CBD=105°,则∠A=65°. 如图,∠DAB、∠EBC、∠ACF是△ABC三个不同的外角,则∠DAB+∠EBC+∠ACF=360°.
如图,∠DAB、∠EBC、∠ACF是△ABC三个不同的外角,则∠DAB+∠EBC+∠ACF=360°.