题目内容
 如图,AE∥BD,C是BD上的点,且AB=BC,∠ACD=130°,则∠EAB=
如图,AE∥BD,C是BD上的点,且AB=BC,∠ACD=130°,则∠EAB=考点:平行线的性质,等腰三角形的性质
专题:
分析:根据邻补角的定义求出∠ACB,再根据等边对等角可得∠ACB=∠CAB,然后求出∠B,再根据两直线平行,内错角相等可得∠EAB=∠B.
解答:解:∵∠ACD=130°,
∴∠ACB=180°-130°=50°,
∵AB=BC,
∴∠ACB=∠CAB,
∴∠B=180°-2×50°=80°,
∵AE∥BD,
∴∠EAB=∠B=80°.
故答案为:80°.
∴∠ACB=180°-130°=50°,
∵AB=BC,
∴∠ACB=∠CAB,
∴∠B=180°-2×50°=80°,
∵AE∥BD,
∴∠EAB=∠B=80°.
故答案为:80°.
点评:本题考查了平行线的性质,等腰三角形的性质,三角形的内角和定理,熟记性质并准确识图,理清图中各角度之间的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列函数的图象中,开口最小的是( )
| A、y=-4x2 | ||
| B、y=-2x2 | ||
C、y=
| ||
D、y=
|
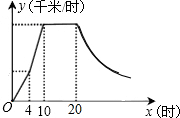 某气象研究中心观测到一场沙尘暴从发生到减弱的过程,开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速y(小时/千米),时间x(小时)成反比例关系地慢慢减弱,结合风速与时间的图象,回答下列问题:
某气象研究中心观测到一场沙尘暴从发生到减弱的过程,开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速y(小时/千米),时间x(小时)成反比例关系地慢慢减弱,结合风速与时间的图象,回答下列问题: 如图,AB∥CD,∠A=45°,且OC=OE,求∠C的度数.
如图,AB∥CD,∠A=45°,且OC=OE,求∠C的度数.