题目内容
12. 如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.
如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.(1)求证:AC平分∠DAB;
(2)若sin∠ABC=$\frac{4}{5}$,求tan∠BDC的值.
分析 (1)先证明AD∥OC,得∠DAC=∠ACO,再根据OA=OC得∠OAC=∠OCA,由此即可证明.
(2)连接BM、OC交于点N,根据sin∠ABC=sin∠BCN=$\frac{4}{5}$=$\frac{BN}{BC}$,设BN=4k,BC=5k,则CN=3k,求出DM,BM,根据tan∠CDB=tan∠DBM=$\frac{DM}{BM}$即可解决问题.
解答 (1)证明: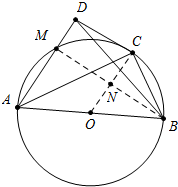 ∵DC是⊙O切线,
∵DC是⊙O切线,
∴OC⊥CD,∵AD⊥CD,
∴AD∥CO,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠OAC=∠ACO,
∴∠DAC=∠CAO,
∴AC平分∠DAB.
(2)解:连接BM、OC交于点N.
∵AB是直径,
∴∠AMB=90°,∵AD∥OC,
∴∠ONB=∠AMB=90°=∠CNB,
∵OC=OB,
∴∠OCB=∠OBC,
∴sin∠ABC=sin∠BCN=$\frac{4}{5}$=$\frac{BN}{BC}$,设BN=4k,BC=5k,则CN=3k,
∵∠CDM=∠DMN=∠DCN=90°,
∴四边形DMNC是矩形,
∴DM=CN=3k,MN=BN=4k,CD∥BM,
∴∠CDB=∠DBM,
∴tan∠CDB=tan∠DBM=$\frac{DM}{BM}$=$\frac{3k}{8k}$=$\frac{3}{8}$.
点评 本题考查切线的性质、垂径定理、勾股定理的高知识,解题的关键是添加辅助线,构造特殊四边形矩形,学会设未知数解决问题,属于中考常考题型.

练习册系列答案
相关题目
17. 如图,数轴上点A表示的数可能是 ( )
如图,数轴上点A表示的数可能是 ( )
 如图,数轴上点A表示的数可能是 ( )
如图,数轴上点A表示的数可能是 ( )| A. | $\sqrt{3}$ | B. | -2.3 | C. | -$\sqrt{3}$ | D. | -2 |
 如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是40cm.求:
如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是40cm.求: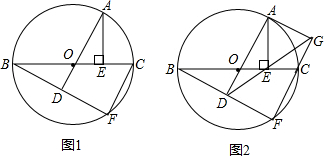
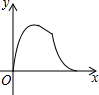
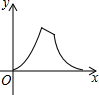
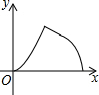
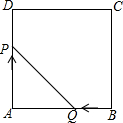 如图,边长为3的正方形ABCD,点P从点A出发以每秒3个单位长度的速度沿A→D→C→B运动,点Q从点B出发以每秒1个单位长度的速度向点A运动,当一个点到达终点时,另一个点也随之停止运动.设△APQ的面积为y,运动时间为x秒,则能大致反映y与x的函败关系的图象是( )
如图,边长为3的正方形ABCD,点P从点A出发以每秒3个单位长度的速度沿A→D→C→B运动,点Q从点B出发以每秒1个单位长度的速度向点A运动,当一个点到达终点时,另一个点也随之停止运动.设△APQ的面积为y,运动时间为x秒,则能大致反映y与x的函败关系的图象是( )