题目内容
12.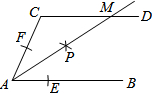 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.若∠ACD=114°,则∠MAB的度数为33°.
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.若∠ACD=114°,则∠MAB的度数为33°.
分析 根据题意可得AM平分∠CAB,再根据平行线的性质可得∠CAB的度数,再根据角平分线的性质可得答案.
解答 解:由题意可得:AM平分∠CAB,
∵AB∥CD,
∴∠C+∠CAB=180°,
∵∠ACD=114°,
∴∠CAB=66°,
∵AM平分∠CAB,
∴∠MAB=33°.
故答案为:33°.
点评 此题主要考查了平行线的性质,以及角平分线的作法,关键是掌握两直线平行,同旁内角互补,以及角平分线的做法.

练习册系列答案
相关题目
7.地球绕太阳公转的速度约是110000千米/时,将110000用科学记数法表示为( )
| A. | 11×104 | B. | 1.1×104 | C. | 1.1×105 | D. | 0.11×106 |
17.下列计算正确的是( )
| A. | 8x+4=12x | B. | 4y-4=y | C. | 4y-3y=y | D. | 3x-x=3 |
4.某校九年级在母亲节倡议“感恩母亲,做点家务”活动.为了解同学们在母亲节的周末做家务情况,年级随机调查了部分同学,并用得到的数据制成如下不完整的统计表.
(1)统计表中的x=80,y=200;
(2)被调查同学做家务时间的中位数是1.5小时,平均数是1.32小时;
(3)年级要组织一次“感恩母亲“的主题级会,级长想从报名的4位同学中随机抽取2位同学在会上谈体会.据统计,报名的4人分别是母亲节的周末做家务1小时的1人、做家务1.5小时的2人、做家务2小时的1人.请你算算选上的2位同学恰好是一位做家务2小时和一位做家务1.5小时的概率.
| 做家务时间 | 频数(人数) | 频率 |
| 0.5 | 24 | 0.12 |
| 1 | 60 | 0.3 |
| 1.5 | x | 0.4 |
| 2 | 36 | 0.18 |
| 合计 | y | 1 |
(2)被调查同学做家务时间的中位数是1.5小时,平均数是1.32小时;
(3)年级要组织一次“感恩母亲“的主题级会,级长想从报名的4位同学中随机抽取2位同学在会上谈体会.据统计,报名的4人分别是母亲节的周末做家务1小时的1人、做家务1.5小时的2人、做家务2小时的1人.请你算算选上的2位同学恰好是一位做家务2小时和一位做家务1.5小时的概率.
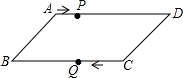 如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD 边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )
如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD 边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )