题目内容
19．
如图，在⊙O中，∠BOC=80°，则∠A等于（ ）| A． | 50° | B． | 20° | C． | 30° | D． | 40° |
分析 因为⊙O是△ABC外接圆，AB是直径，∠ACB=90°，∠A+∠B=90°，又因为∠BOC=80°，OB=OC，所以∠B=∠BCO=50°，所以∠A=40°．
解答 解：∵⊙O是△ABC外接圆，AB是直径，
∴∠ACB=90°，
∴∠A+∠B=90°，
∵OB=OC，
∴∠B=∠BCO，
∵∠BOC=80°，
∴∠B=∠BCO=50°
∴∠A=40°．
故选D．
点评 此题目考查了圆周角定理的推论：直径所对的圆周角是直角．并且解题时注意题目中的隐含条件，即圆的半径处处相等．
练习册系列答案
相关题目
如图，菱形ABCD中，AB=4，∠ABC=60°，点E、F、G分别为线段BC，CD，BD上的任意一点，则EG+FG的最小值为2$\sqrt{3}$．
7．关于$\sqrt{8}$的叙述错误的是（ ）
| A． | $\sqrt{8}$=2$\sqrt{2}$ | B． | 面积为8的正方形边长为$\sqrt{8}$ | ||
| C． | 在数轴上可以找到表示$\sqrt{8}$的点 | D． | $\sqrt{8}$是有理数 |
4．在平面直角坐标系中，以点（3，2）为圆心，2为半径的圆与坐标轴的位置关系为（ ）
| A． | 与x轴相离、与y轴相切 | B． | 与x轴、y轴都相离 | ||
| C． | 与x轴相切、与y轴相离 | D． | 与x轴、y轴都相切 |
8．如果某个斜坡的坡度是1：$\sqrt{3}$，那么这个斜坡的坡角为（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
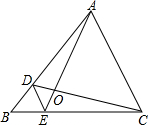如图，D、E分别是△ABC的边AB、BC上的点，DE∥AC，若S△BDE：S△CDE=1：3，求S△DOE：S△AOC的值．