题目内容
14．
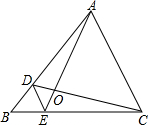如图，D、E分别是△ABC的边AB、BC上的点，DE∥AC，若S△BDE：S△CDE=1：3，求S△DOE：S△AOC的值．
分析 由已知得出BE：BC=1：4；证明△DOE∽△AOC，得到$\frac{DE}{AC}=\frac{1}{4}$，由相似三角形的性质即可解决问题．
解答 解：∵S△BDE：S△CDE=1：3，
∴BE：EC=1：3；
∴BE：BC=1：4；
∵DE∥AC，
∴△DOE∽△AOC，
∴$\frac{DE}{AC}=\frac{BE}{BC}$=$\frac{1}{4}$，
∴S△DOE：S△AOC=（$\frac{1}{4}$）=$\frac{1}{16}$．
点评 本题主要考查了相似三角形的判定及其性质的应用问题；熟练掌握相似三角形的判定与性质，证出BE：BC=1：4是解决问题的关键解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
19．
如图，在⊙O中，∠BOC=80°，则∠A等于（ ）
如图，在⊙O中，∠BOC=80°，则∠A等于（ ）| A． | 50° | B． | 20° | C． | 30° | D． | 40° |
6．某市水果批发部门欲将A市的一批水果运往本市销售，有火车和汽车两种运输方式，运输过程中的损耗均为200元/时，火车与汽车在路上耽误的时间分别为2小时和3.1小时，其它主要参考数据如下：
（1）如果A市与本市之间的距离为x千米，请分别求出选择火车的总费用y1（元）和选择汽车的总费用y2（元）关于x（千米）的函数关系式（总费用=运费+装卸费用+损耗）；
（2）你若是该市水果批发部门的经理，要想将这种水果运往本市销售，你将选择哪种运输方式比较合算呢？
| 运输工具 | 途中平均速度 （千米/时） | 运费 （元/千米） | 装卸费用 （元） |
| 火车 | 100 | 15 | 2000 |
| 汽车 | 80 | 20 | 900 |
（2）你若是该市水果批发部门的经理，要想将这种水果运往本市销售，你将选择哪种运输方式比较合算呢？
3．下列各式中与（a-1）2相等的是（ ）
| A． | a2-1 | B． | a2+2a+1 | C． | a2-2a-1 | D． | （1-a）2 |
4．某商场经营某种品牌的玩具，购进时的单价是20元，根据市场调查：在一段时间内，销售单价是30元时，销售量是500件，而销售单价每上涨1元，就会少售出10件玩具．
（1）不妨设该种品牌玩具的销售单价为x元（x＞30），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在表格中：
（2）在第（1）问的条件下，若商场获得了8750元销售利润，求该玩具销售单价x应定为多少元？
（3）在第（1）问的条件下，若玩具厂规定该品牌玩具销售单价不低于32元，且商场要完成不少于400件的销售任务，求：商场销售该品牌玩具获得最大利润是多少？
（1）不妨设该种品牌玩具的销售单价为x元（x＞30），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在表格中：
| 销售单价（元） | x（x＞30） |
| 销售量y（件） | -10x+800 |
| 销售玩具获得利润w（元） | -10x2+1000x-16000 |
（3）在第（1）问的条件下，若玩具厂规定该品牌玩具销售单价不低于32元，且商场要完成不少于400件的销售任务，求：商场销售该品牌玩具获得最大利润是多少？