题目内容
4.《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是6步.分析 设三角形△ABC,由勾股定理可求得直角三角形的斜边,设内切圆的半径为r,由S△ABC=$\frac{1}{2}$(AB+BC+CA)•r可求得半径,则可求得直径.
解答 解:
设三角形为△ABC,∠C=90°,AC=8,BC=15,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+1{5}^{2}}$=17,
设内切圆的半径为r,则S△ABC=$\frac{1}{2}$(AB+BC+CA)•r,
∴$\frac{1}{2}$AC•BC=$\frac{1}{2}$(AB+BC+CA)•r,即$\frac{1}{2}$×8×15=$\frac{1}{2}$×(8+15+17)•r,
解得r=3,
∴内切圆的直径是6步,
故答案为:6.
点评 本题主要考查三角形的内切圆,利用等积法得到关于内切圆半径的方程是解题的关键.

练习册系列答案
相关题目
 如图,小明家(A点)在一条河流(直线l,宽度忽略不计)的一侧,在河流的同侧有一公园(B点),小风家恰好关于此河流与小明家对称
如图,小明家(A点)在一条河流(直线l,宽度忽略不计)的一侧,在河流的同侧有一公园(B点),小风家恰好关于此河流与小明家对称 如图,圆O的弦AB垂直平分半径OC,若圆O的半径为4,则弦AB的长等于4$\sqrt{3}$.
如图,圆O的弦AB垂直平分半径OC,若圆O的半径为4,则弦AB的长等于4$\sqrt{3}$.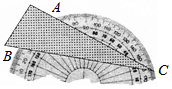 将一个三角形纸板按如图所示的方式放置一个破损的量角器上,使点C落在半圆上,若点A、B处的读数分别为65°、20°,则∠ACB的大小为22.5°.
将一个三角形纸板按如图所示的方式放置一个破损的量角器上,使点C落在半圆上,若点A、B处的读数分别为65°、20°,则∠ACB的大小为22.5°.
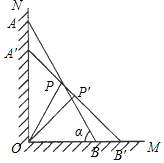 如图,一架长2米的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面的倾斜角α为60°.当A点下滑到A′点,B点向右滑行到B′点时,梯子AB的中点P也随之运动到P′点.若∠POP′=15°,则AA′的长$\sqrt{3}$-$\sqrt{2}$.
如图,一架长2米的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面的倾斜角α为60°.当A点下滑到A′点,B点向右滑行到B′点时,梯子AB的中点P也随之运动到P′点.若∠POP′=15°,则AA′的长$\sqrt{3}$-$\sqrt{2}$.