题目内容
3. 如图,矩形ABCD的对角线AC,BD交于点O,E为CD的中点,延长OE至点F,使OE=EF.
如图,矩形ABCD的对角线AC,BD交于点O,E为CD的中点,延长OE至点F,使OE=EF.(1)求证:四边形OBCF为平行四边形;
(2)求证:△CEF∽△ABC.
分析 (1)根据矩形的性质可得O为BD中点,再由E为CD中点可得EO为中位线,根据中位线定理可得EO∥BC,BC=2EO,然后再证明OF=BC,进而可得四边形OBCF为平行四边形;
(2)首先证明∠CEF=∠DCB=90°,再证明∠F=∠OCB,进而可判定△CEF∽△ABC.
解答 证明:(1)∵矩形ABCD的对角线交于点O,
∴O为BD中点,
∵E为CD中点,
∴△DBC中,EO为中位线,
∴EO∥BC,BC=2EO,
∴EO=EF,
∴FO=EO+EF=2EO,
∴OF=BC,
又OF∥BC,
∴四边形OBCF为平行四边形;
(2)矩形ABCD中,∠DCB=90°.
∵EO∥BC,
∴∠CEF=∠DCB=90°,
在?OBCF中,∠F=∠OBC,
矩形ABCD中,AC=BD,
∴$\frac{1}{2}$AC=$\frac{1}{2}$BD,即CO=BO,
∴∠OBC=∠OCB,
∴∠F=∠OCB,
∴△CEF∽△ABC.
点评 此题主要考查了平行四边形的判定和性质,以及相似三角形的判定,关键是掌握一组对边平行且相等的四边形是平行四边形;有两组角对应相等的两个三角形相似.

练习册系列答案
相关题目
11. 如图,已知△ABC中,点D在AB上,且CD=AD=BD,点F在BC上,过D作DE⊥DF交AC于E,过F作FG⊥AB于G,以下结论:①△ABC为直角三角形,②BF2+DG2=DF2+BG2,③AE2+BF2=CE2+CF2,④AG2=AC2+BG2,其中结论正确的序号是( )
如图,已知△ABC中,点D在AB上,且CD=AD=BD,点F在BC上,过D作DE⊥DF交AC于E,过F作FG⊥AB于G,以下结论:①△ABC为直角三角形,②BF2+DG2=DF2+BG2,③AE2+BF2=CE2+CF2,④AG2=AC2+BG2,其中结论正确的序号是( )
 如图,已知△ABC中,点D在AB上,且CD=AD=BD,点F在BC上,过D作DE⊥DF交AC于E,过F作FG⊥AB于G,以下结论:①△ABC为直角三角形,②BF2+DG2=DF2+BG2,③AE2+BF2=CE2+CF2,④AG2=AC2+BG2,其中结论正确的序号是( )
如图,已知△ABC中,点D在AB上,且CD=AD=BD,点F在BC上,过D作DE⊥DF交AC于E,过F作FG⊥AB于G,以下结论:①△ABC为直角三角形,②BF2+DG2=DF2+BG2,③AE2+BF2=CE2+CF2,④AG2=AC2+BG2,其中结论正确的序号是( )| A. | ①② | B. | ①④ | C. | ①②③ | D. | ①②③④ |
18.有一列数a,b,c,d,…,从第二个数开始,每一个数都等于1与它前面那个数的倒数的差.若第一个数a等于2,则第2014个数等于( )
| A. | 2014 | B. | 2 | C. | $\frac{1}{2}$ | D. | -1 |

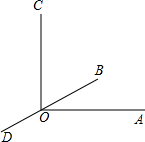 如图,已知∠AOC=90°,直线BD过点O,∠COD=115°15′,则∠AOB=25°15′.
如图,已知∠AOC=90°,直线BD过点O,∠COD=115°15′,则∠AOB=25°15′. 解不等式2(x+1)-1≥4x+3,并把它的解集在数轴上表示出来.
解不等式2(x+1)-1≥4x+3,并把它的解集在数轴上表示出来.