题目内容
6．
如图，在△ABC中，AB=AC，过点A作AD∥BC．若∠1=70°，则∠BAC的大小为（ ）| A． | 30° | B． | 40° | C． | 50° | D． | 70° |
分析 根据平行线的性质求出∠C，根据等腰三角形的性质得出∠B=∠C=70°，根据三角形内角和定理求出即可．
解答 解：∵AB=AC，
∴∠B=∠C，
∵AD∥BC，∠1=70°，
∴∠C=∠1=70°，
∴∠B=70°，
∴∠BAC=180°-∠B-∠C=180°-70°-70°=40°，
故选B．
点评 本题考查了三角形内角和定理，等腰三角形的性质，平行线的性质的应用，解此题的关键是求出∠C的度数和得出∠B=∠C，注意：三角形内角和等于180°，两直线平行，内错角相等．
练习册系列答案
相关题目
16．
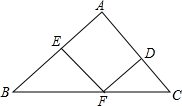如图，在△ABC中，点D、E、F分别是三条边上的点，EF∥AC，DF∥AB，∠B=45°，∠C=60°．则∠EFD=（ ）
如图，在△ABC中，点D、E、F分别是三条边上的点，EF∥AC，DF∥AB，∠B=45°，∠C=60°．则∠EFD=（ ）| A． | 80° | B． | 75° | C． | 70° | D． | 65° |
如图，已知△ABC，请用尺规过点A作一条直线，使其将△ABC分成面积相等的两部分．（保留作图痕迹，不写作法）
如图，PA为⊙O的切线，A为切点，B是OP与⊙O的交点．若∠P=20°，OA=3，则$\widehat{AB}$的长为$\frac{7}{6}$π（结果保留π）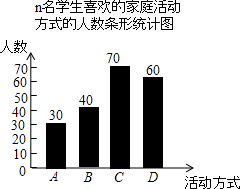
在“世界家庭日”前夕，某校团委随机抽取了n名本校学生，对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查．问卷中的家庭活动方式包括：
