题目内容
10. 如图所示是上海东方明珠广播电视塔的一部分,若塔座所形成的直角三角形的直角边长分别是a,b,则斜边长为$\sqrt{{a}^{2}+{b}^{2}}$,圆形的球体在平面图上的面积为S,则半径为$\frac{\sqrt{πS}}{π}$.
如图所示是上海东方明珠广播电视塔的一部分,若塔座所形成的直角三角形的直角边长分别是a,b,则斜边长为$\sqrt{{a}^{2}+{b}^{2}}$,圆形的球体在平面图上的面积为S,则半径为$\frac{\sqrt{πS}}{π}$.
分析 根据勾股定理和二次根式的性质解答即可.
解答 解:直角三角形的直角边长分别是a,b,则斜边长为$\sqrt{{a}^{2}+{b}^{2}}$,
圆形的球体在平面图上的面积为S,
∵S=πR2,
则半径为$\frac{\sqrt{πS}}{π}$,
故答案为:$\sqrt{{a}^{2}+{b}^{2}}$;$\frac{\sqrt{πS}}{π}$.
点评 本题考查的是勾股定理的应用和二次根式的化简,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
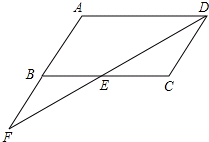 如图.在平行四边形ABCD中,点F在AB的延长线上,且BF=AB.连接FD,交BC于点E
如图.在平行四边形ABCD中,点F在AB的延长线上,且BF=AB.连接FD,交BC于点E 如图,甲楼每层高都是3.1米,乙楼高40米,从甲楼的第6层往外看乙楼楼顶,仰角为30°,两楼相距AB有多少米?(结果精确到0.1米)
如图,甲楼每层高都是3.1米,乙楼高40米,从甲楼的第6层往外看乙楼楼顶,仰角为30°,两楼相距AB有多少米?(结果精确到0.1米)