��Ŀ����
5����ͼ����֪����P��ԭ��O������������ĸ�������ÿ��1����λ���ȵ��ٶ��˶�������Q��ԭ��O���������������������ÿ��2����λ���ȵ��ٶ��˶����˶���ʱ��Ϊt���룩����1����t=2ʱ����PQ�ij�������A���߶�PQ���е㣬���A��ʾ�����Ƕ��٣�
��2����t=3ʱ����PQ�ij�������A���߶�PQ���е㣬���A��ʾ�����Ƕ��٣�
��3����t=nʱ����PQ�ij�������A���߶�PQ���е㣬���A��ʾ�����Ƕ��٣����ú�n�Ĵ���ʽ��ʾ��
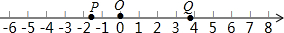
���� ��1�����ݵ�P�˶��ٶȺ͵�Q�˶��ٶȣ�������������˶��ĵ�λ���ȣ����ɽ��
��2�����ݵ�P�˶��ٶȺ͵�Q�˶��ٶȣ�������������˶��ĵ�λ���ȣ����ɽ��
��3�����ݵ�P�˶��ٶȺ͵�Q�˶��ٶȣ�������������˶��ĵ�λ���ȣ����ɽ��
��� �⣺��1����t=2ʱ������P��ԭ��O������������ĸ������˶�2����λ���ȣ�����Q��ԭ��O��������������������˶�4����λ���ȣ���PQ=2+4=6��
����A���߶�PQ���е㣬���A��ʾ�����ǣ���-2+4����2=1��
��2����t=3ʱ������P��ԭ��O������������ĸ������˶�3����λ���ȣ�����Q��ԭ��O��������������������˶�6����λ���ȣ���PQ=3+6=9��
����A���߶�PQ���е㣬���A��ʾ�����ǣ���-3+6����2=1.5��
��3����t=nʱ������P��ԭ��O������������ĸ������˶�n����λ���ȣ�����Q��ԭ��O��������������������˶�2n����λ���ȣ���PQ=n+2n=3n��
����A���߶�PQ���е㣬���A��ʾ�����ǣ���-n+2n����2=$\frac{n}{2}$��
���� ���⿼�������ᣬ�������Ĺؼ��Ǽ�����������˶��ĵ�λ���ȣ�

��ϰ��ϵ�д�
�����Ŀ
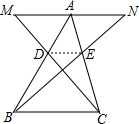 ��ͼ��MN������ABC�Ķ���A��MN��BC��AM=AN��MC��AB��D��NB��AC��E��
��ͼ��MN������ABC�Ķ���A��MN��BC��AM=AN��MC��AB��D��NB��AC��E�� ��ͼ��ʾ���Ϻ���������㲥��������һ���֣����������γɵ�ֱ�������ε�ֱ�DZ߳��ֱ���a��b����б�߳�Ϊ$\sqrt{{a}^{2}+{b}^{2}}$��Բ�ε�������ƽ��ͼ�ϵ����ΪS����뾶Ϊ$\frac{\sqrt{��S}}{��}$��
��ͼ��ʾ���Ϻ���������㲥��������һ���֣����������γɵ�ֱ�������ε�ֱ�DZ߳��ֱ���a��b����б�߳�Ϊ$\sqrt{{a}^{2}+{b}^{2}}$��Բ�ε�������ƽ��ͼ�ϵ����ΪS����뾶Ϊ$\frac{\sqrt{��S}}{��}$��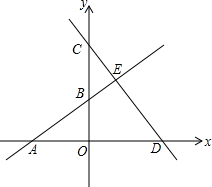 ��ͼ��ֱ��AB��y=kx+b��x���ڵ�A��-3��0������y���ڵ�B��0��2������ֱ��CD�ڵ�E����E��ĺ�����Ϊ3��ֱ��CD��x���ڵ�D��10��0����
��ͼ��ֱ��AB��y=kx+b��x���ڵ�A��-3��0������y���ڵ�B��0��2������ֱ��CD�ڵ�E����E��ĺ�����Ϊ3��ֱ��CD��x���ڵ�D��10��0����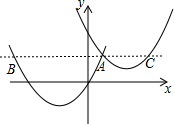 ��ͼ�������κ���y2=��x-$\frac{7}{4}$��2-2��ͼ����ƽ��m����λ������κ���y1=��x+2��2-4��ͼ���ཻ�ڵ�A����A��x���ƽ���߷ֱ�y1��y2�ڵ�B��C����AC=$\frac{1}{2}$BAʱ��m��ֵ��$\frac{43}{16}$��
��ͼ�������κ���y2=��x-$\frac{7}{4}$��2-2��ͼ����ƽ��m����λ������κ���y1=��x+2��2-4��ͼ���ཻ�ڵ�A����A��x���ƽ���߷ֱ�y1��y2�ڵ�B��C����AC=$\frac{1}{2}$BAʱ��m��ֵ��$\frac{43}{16}$��