Question

15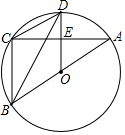．如图，⊙O是△ABC的外接圆，AB为直径，D是⊙O上一点，且OD⊥AC于点E，连结BD、CD．
（1）求证：BD平分∠ABC；
（2）当∠ODB=30°时，求证：四边形BCDO是菱形．

Answer 1

分析 （1）根据垂径定理证明$\widehat{CD}=\widehat{AD}$，然后根据等弧所对的圆周角相等证得；
（2）证明△OBC和△COD都是等边三角形，则四边形BCDO的四边相等，据此即可证得四边形是菱形．

解答 解：（1）连接OC．
∵OD⊥AC，
∴$\widehat{CD}=\widehat{AD}$，
∴∠AOD=∠COD，
∴∠ABD=∠CBD，即BD平分∠ABC；
（2）∵OD=OB，
∴∠OBD=∠ODB=30°，
又∵BD平分∠ABC，
∴∠CBD=2∠OBD=60°，∠BOD=120°，
又∵OC=OB，
∴△OBC是等边三角形，
∴OB=OC=BC，∠BOC=60°，
∴∠COD=60°，
又∵OC=OD，
∴△COD是等边三角形，
∴OC=OD=CD，
∴OD=CD=BC=OB，
∴四边形BCDO是菱形．

点评 本题考查了垂径定理和菱形的判定，正确证明△OBC和△COD都是等边三角形是关键．